
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры моделей линейного программирования
|
|
|
|
Модели задач линейного программирования
2.1. Линейное программирование как инструмент
математического моделирования экономики
Линейное программирование традиционно считается одним из разделов исследования операций, который изучает методы нахождения условного экстремума функций многих переменных. Практика показывает, что значительное количество экономических процессов достаточно полно описывается линейными моделями, а, следовательно, линейное программирование как аппарат, позволяющий отыскивать условный экстремум на множестве, заданном линейными уравнениями и неравенствами, играет важную роль при анализе этих процессов.
Литература:
1. Ширяев В.И. Исследование операций и численные методы оптимизации. – М.: Издательская группа URSS, 2006.
2. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. – М.: Издательская группа URSS, 2009. – 288 с.
3. Шапкин А.С., Шапкин В.А. Математические методы и модели исследования операций. – М.: Дашков и К, 2009. – 400 с.
В экономико-математических моделях линейного программирования часто в качестве оценки качества решения используются такие показатели, как: прибыль, себестоимость, объем производства.
Ниже рассмотрим несколько ситуаций, исследование которых возможно с применением средств линейного программирования.
1. Задача о раскрое материала. На обработку поступает материал одного образца в количестве 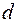 единиц. Требуется изготовить из него
единиц. Требуется изготовить из него 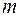 разных комплектующих изделий в количествах, пропорциональных числам
разных комплектующих изделий в количествах, пропорциональных числам  . Каждая единица материала может быть раскроена
. Каждая единица материала может быть раскроена 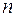 различными способами, при этом использование
различными способами, при этом использование 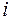 -го способа
-го способа 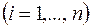 дает
дает 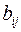 единиц
единиц  -го изделия
-го изделия 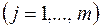 .
.
Требуется найти план раскроя, обеспечивающий максимальное количество комплектов 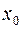 .
.
|
|
|
Экономико-математическая модель этой задачи может быть сформулирована следующим образом. Обозначим  число единиц материалов, раскраиваемых
число единиц материалов, раскраиваемых 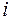 -м способом
-м способом 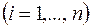 .
.
Учитывая, что общее количество материала равно сумме его единиц, раскрываемых различными способами, получим:
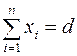 . (1.1)
. (1.1)
Условие комплектности выразится уравнениями:
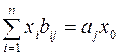 ,
, 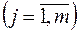 . (1.2)
. (1.2)
Очевидно, что
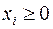 ,
, 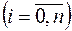 . (1.3)
. (1.3)
Целью является определить такое решение  , удовлетворяющее ограничениям (1.1) – (1.3), при котором функция
, удовлетворяющее ограничениям (1.1) – (1.3), при котором функция 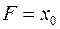 принимает максимальное решение.
принимает максимальное решение.
Проиллюстрируем рассмотренную задачу следующим примером.
Для изготовления брусьев длиной 1,5 м, 3 м и 5 м в соотношении 2:1:3 на распил поступило 200 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов. Чтобы сформулировать соответствующую оптимизационную задачу линейного программирования, определим все возможные способы распила бревен, указав соответствующее число получаемых при этом брусьев (табл.1.1).
Обозначим через  число бревен, распиленных
число бревен, распиленных 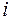 -м способом
-м способом 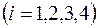 ;
; 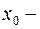 число комплектов брусьев.
число комплектов брусьев.
Таблица 1.1
Способ
распила, 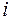
| Число получаемых брусьев различной длины 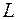
| ||
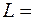 1,5 1,5
| 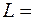 3,0 3,0
| 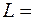 5,0 5,0
| |
| - | - | ||
| - | |||
| - | - | ||
| - | - |
С учетом того, что все бревна должны быть распилены, а число брусьев каждого размера должно удовлетворять условию комплектности, оптимизационная экономико-математическая модель примет следующий вид:
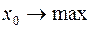
при ограничениях:
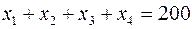 ,
,
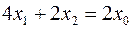 , (1.4)
, (1.4)
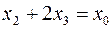 ,
,
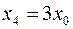 ,
,
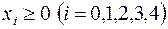 .
.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1185; Нарушение авторских прав?; Мы поможем в написании вашей работы!