Структура общего решения неоднородной системы линейных уравнений

Рассмотрим теперь неоднородную систему линейных уравнений с прямоугольной матрицей :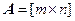

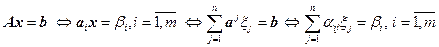. (4.4.1)

Наряду с матрицей системы (4.4.1) рассмотрим расширенную матрицу .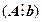

Теорема 4.4.1 (теорема Кронекера-Капелли). Для того чтобы система (4.4.1) была совместной, необходимо и достаточно, чтобы ранг матрицы системы совпадал с рангом расширенной матрицы, т. е. .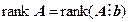

Доказательство. Необходимость. Пусть система (4.4.1) имеет решение 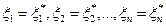. Тогда 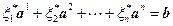, следовательно, столбец 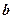разложен по столбцам 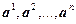и 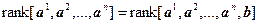, т. е.

.

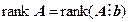Достаточность. Предположим, что 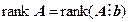. В матрице системы существует столбцовый базис, содержащий максимальное число линейно независимых столбцов матрицы 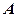. Указанное число по условию не меняется после присоединения к столбцам матрицы 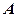столбца 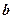, поэтому его можно разложить по базису, т. е.

.

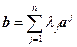Но тогда столбец 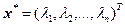есть решение системы (4.4.1), поэтому она является совместной.

Теорема 4.4.2. Общее решение системы (4.4.1) равно сумме некоторого решения неоднородной системы, называемого частным решением, и общего решения соответствующей однородной системы.

Доказательство. Зафиксируем произвольное решение неоднородной системы (4.4.1) 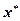. Тогда имеем тождество 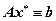. Следовательно, систему (4.4.1) можно представить в виде 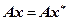, отсюда 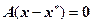. Если ранг матрицы A равен r, то фундаментальная система решений полученной однородной системы состоит из 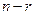линейно независимых столбцов 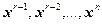, а ее общее решение записывается в ви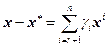де , где 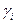— произвольные постоянные. Таким образом, общее решение системы (4.4.1) имеет вид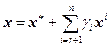

Лемма 4.4.1. Для любых чисел 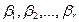и произвольных линейно независимых столбцов 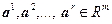система линейных уравнений 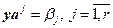всегда имеет решение.

Доказательство. Так как столбцы матрицы 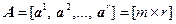линейно независимы, то в ней существует ровно 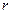линейно независимых строк, образующих строчечный базис. Пусть для определенности этим базисом в 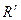являются 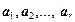. Тогда для 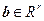справедливо 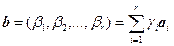, т. е.

является искомым решением системы.

Следствие 4.4.1. Если 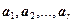линейно независимые строки, то для любых чисел 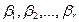система линейных уравнений 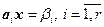всегда имеет решение.

Дата добавления: 2014-01-05