Метод Гаусса. Рассмотрим неоднородную систему линейных уравнений с прямоугольной матрицей :

Рассмотрим неоднородную систему линейных уравнений с прямоугольной матрицей :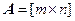

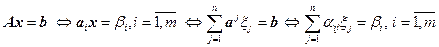, (4.5.1)

где матрица 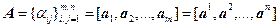, столбцы , .

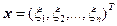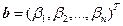Теорема 4.5.1. Любая совместная система линейных уравнений посредством элементарных преобразований и, возможно, изменения нумерации неизвестных приводится к системе с трапециевидной матрицей.

Доказательство. По условию система (4.5.1) является совместной, поэтому допустим, что 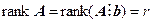. В матрице A существует ровно 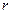линейно независимых строк 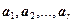, образующих строчечный базис. Тогда для любого 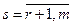, , 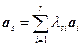поэтому систему (4.5.1) можно переписать в виде

,

, .

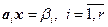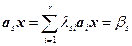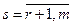Умножая каждое i- ое уравнение (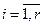) на число 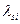, и, затем вычитая из s- го уравнения (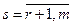), получаем систему

,

, .

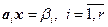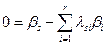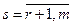Так как 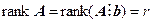, то для любого 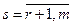числа 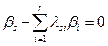, ибо в противном случае система окажется несовместной. Тогда, очевидно, что система (4.5.1) равносильна системе

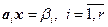. (4.5.2)

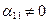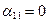Рассмотрим теперь систему (4.5.2). Пусть коэффициент (если , то перестановкой местами уравнений всегда можно добиться выполнения условия ).

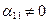Умножая первое уравнение системы на число 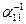, получаем

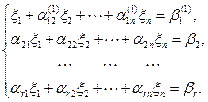
Вычтем из каждого уравнения, начиная со второго, первое уравнение, предварительно умноженное соответственно на 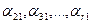, получаем

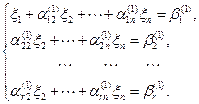
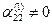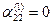Предположим, что (если , то перестановкой местами уравнений, начиная с третьего, всегда можно добиться выполнения условия ).

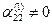Умножая второе уравнение на величину 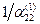, получаем

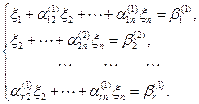
Вычитая второе уравнение, предварительно умноженное 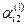, из i- го уравнения (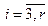), а, затем повторяя описанную процедуру, получаем систему

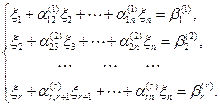
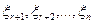Если , то переменные называются свободными, им можно придавать произвольные значения, а потом через них выразить .

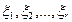Когда справедливо равенство 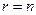, то в силу совместности системы (4.5.1) система (4.5.2) имеет единственное решение.

Заметим, что если выполнено соотношение 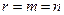, то матрица системы приводится к треугольному виду.

Преобразование системы к системе с трапециевидной матрицей указанным выше способом называется прямым ходом метода Гаусса, а вычисление последовательно значений называется обратным ходом.

Дата добавления: 2014-01-05