Векторное произведение векторов

Proof.

curves equal to

Let equalities hold

1. The first curves we transport to parallel, and point with point osculate.

2. Then vectors with vectors osculate that in point we translate curves. Then the transformations

, (*)

To prove the theorem we have to show that the equality in any decision parameter. Let us look at it this

We solve this scalar product, and use equation, explore

(*) performed

Then for every

then

This equation is performed when exactly former, except during the <3 is quiche.

so

three Frenet vectors under equal.

Now we point out that the vector functions areequal then we deduce following differential equation, and lets sove it

(*)

In the first condition, there, and so

The theorem is proved

Определение 3.18.1. Векторным произведением вектора на вектор называется вектор 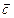, обозначаемый символом =и определяемый следующим образом:

1) модуль вектора равен произведению модулей векторов и на синус угла между этими векторами =sin j, где .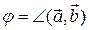

2) вектор перпендикулярен каждому из векторов и ;

3) вектор направлен так, что упорядоченная тройка векторов ,,является правой (рис. 3.18.1).

Рис.3.18.1

Ясно, что если хотя бы один из векторов и нулевой, то их векторное произведение есть нулевой вектор.

Наряду с введенным обозначением будем использовать, когда это удобно, и другую форму записи векторного произведения [,].

Лемма 3.18.1. Векторное произведение двух неколлинеарных векторов и 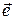, причем — произвольный вектор, а 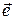— единичный вектор, равно вектору 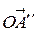, построенному следующим образом:

1) векторы и 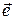приведены к общему началу О;

2) вектор получен в результате проектирования вектора на плоскость p, перпендикулярную к вектору 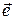и проходящую через О;

3) вектор 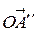построен с помощью поворота вектора в плоскости p на угол, равный 90°, так чтобы упорядоченная тройка , , 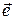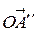была правой.

Доказательство. Пусть j — угол между векторами и 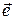, a — угол между вектором и его проекцией . Нетрудно видеть, что вектор 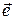лежит в той же плоскости, что и векторы и (рис. 3.18.2, 3.18.3). Поэтому векторы и 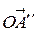перпендикулярны плоскости, определяемой векторами 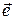, , и, следовательно, они коллинеарны. Кроме того,

Рис. 3.18.2

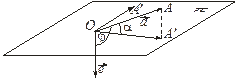Рис. 3.18.3

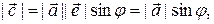
поэтому 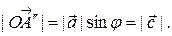По построению тройка векторов , , 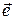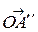— правая. В силу того, что 0 < a < 90°, тройка векторов , , 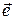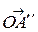также будет правой. Однако, по определению векторного произведения тройка ,,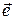является правой, поэтому 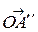, отсюда =.

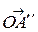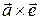Теорема 3.18.1. Необходимым и достаточным условием коллинеарности двух ненулевых векторов и является равенство .

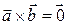Доказательство. Необходимость. Пусть и коллинеарны. Тогда угол j между ними равен 0, если они сонаправлены и равен 180°, если они противоположно направлены, но в любом случае

Достаточность. Пусть следовательно,

|| = 0 sin j = 0 j = pk, k Î Z .

Теорема 3.18.2 (свойства векторного произведения). Для любых трех векторов 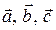и произвольного числа l справедливы соотношения:

1. 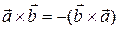(антикоммутативность);

2. (ассоциативность относительно числового
множителя);

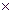
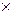
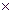
3. ( + )= + (дистрибутивность относительно суммы
векторов);

4. =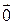(для любого вектора ).

Доказательство. Свойство 1. Будем считать, что векторы и неколлинеарные, иначе свойство 1 очевидно. Пусть векторы =и 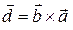, а j — угол между и . Ясно, что

.

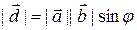
Понятно, что векторы и коллинеарные, так как они перпендикулярны плоскости, в которой лежат векторы и . Согласно определению векторного произведения, упорядоченные тройки векторов ,,и ,,являются правыми, а это влечет противоположную направленность векторов и (рис. 3.18.4). Следовательно, векторы и — противоположные, т. е. .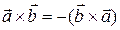

Свойство 2. Будем считать, что векторы и неколлинеарные, l ¹ 0. Пусть 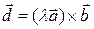, , 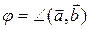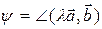. Ясно (рис.3.18.5, 3.18.6), что

Векторы и 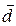коллинеарны, так как они перпендикулярны плоскости, определяемой векторами и .

.

Если

l > 0 .

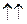
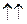
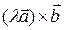
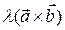
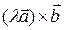Если

l < 0 .

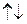
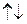
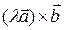
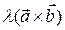
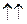
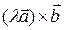Таким образом,

, .

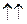
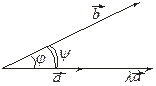Рис. 3.18.5

Рис. 3.18.6

Свойство 3. Будем считать, что , и . Докажем сначала справедливость равенства 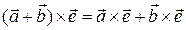, где 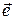— единичный вектор. Будем предполагать, что векторы ,,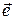некомпланарны.

Приведем векто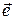ры ,,к общему началу О. Спроектируем векторы ,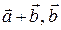на плоскость p, перпендикулярную вектору 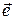и проходящую через точку О. Получаем соответственно векторы 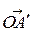,,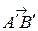(рис. 3.18.7). Построим векторы ,,как указано в лемме. По определению суммы векторов =+. Но в силу леммы
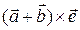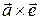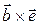=, =, =, поэтому =+.

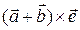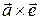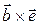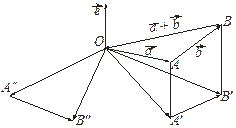
Рис. 3.18.7

Ясно, что если 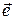,,компланарны, то доказательство и соответствующий чертеж значительно упрощаются.

Пусть 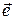— орт вектора , тогда 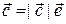, поэтому

Свойство 4. Справедливость указанного соотношения непосредственно вытекает из определения векторного произведения.

Доказанные свойства позволяют при векторном перемножении векторных многочленов выполнять действия почленно и производить объединение числовых множителей. При этом нужно тщательно следить за порядком векторных множителей.

Теорема 3.18.3. Векторное произведение векторов 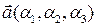и 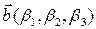, заданных своими аффинными координатами, вычисляется по формуле

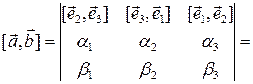
. (3.18.1)

Доказательство. По определению аффинных координат , , поэтому с учетом свойств векторного произведения

=

=

.

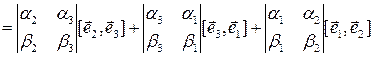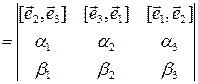Следствие 3.18.1. Векторное произведение векторов и 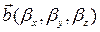, заданных своими декартовыми прямоугольными координатами, находится по формуле

(3.18.2)

Доказательство. Пусть 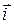,,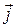— ортонормированный базис декартовой прямоугольной системы координат. Поскольку 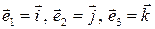, то в формуле (3.18.1) 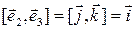, , 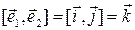. С учетом равенств 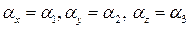, получаем формулу (3.18.2).

Теорема 3. 18. 4. Модуль векторного произведения двух неколлинеарных векторов и равен площади S параллелограмма, построенного на этих векторах, после приведения их к общему началу, т. е.

|| = S. (3.18.3)

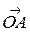Доказательство. Известно, что площадь параллелограмма равна произведению длин его смежных сторон на синус угла между ними (рис. 3.18.8) SOBDA = , где j — угол между векторами и . Отсюда = SOBDA.

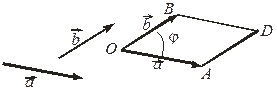
Рис. 3.18.8

Следствие 3.18.2. Векторное произведение , где 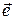— орт векторного произведения , S — площадь параллелограмма, построенного на приведенных к общему началу векторах и .

Следствие 3.18.3. Площадь параллелограмма, построенного на двух неколлинеарных векторах и 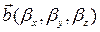, заданных своими прямоугольными декартовыми координатами и приведенных к общему началу, определяется по формуле

S = .

Указанное равенство вытекает из соотношений (3.18.3), (3.18.2) и формулы для определения модуля вектора.

Дата добавления: 2014-01-05