Двойное векторное произведение

Определение 3.20.1. Двойным векторным произведением трех векторов 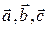называется вектор

Теорема 3.20.1. Двойное векторное произведение равно среднему вектору произведения, умноженному на скалярное произведение двух остальных, минус другой вектор внутреннего произведения, умноженный на скалярное произведение двух остальных, т. е.

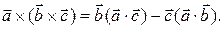(3.20.1)

Доказательство. Пусть , где 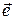— орт векторного произведения, 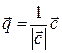— орт вектора .

Введем вспомогательный орт , причем тройка векторов — правая, а также углы (рис. 3.20.1). Площадь параллелограмма, построенного на векторах 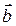и , равна

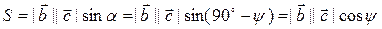. (3.20.2)

Рис. 3.20.1

Пусть 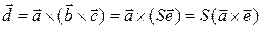. По определению векторного произведения вектор , поэтому 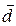лежит в плоскости векторов 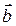и , отсюда 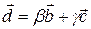. С другой стороны 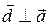, т. е. . Используя выражение для вектора 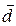, имеем

,

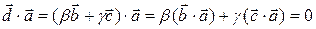отсюда

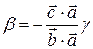
и, окончательно,

. (3.20.3)

Тройка векторов образует ортонормированный базис, в котором вектор представим в виде:

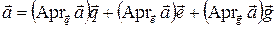. (3.20.4)

Вектор

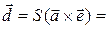
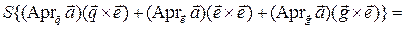
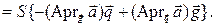(3.20.5)

Сравнивая полученное выражение для вектора 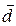с соотношением (3.20.3), имеем тождество

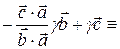
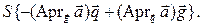
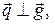
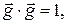
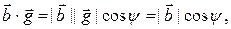
Умножим обе части этого тождества скалярно на вектор . Тогда с учетом соотношений и формулы (3.20.2) имеем

После всех сокращений получаем 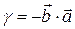, следовательно, 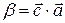, а тогда из формулы (3.20.3) имеем (3.20.1).

Следствие 3.20.1. Справедлива формула .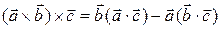

Доказательство. С учетом свойств векторного произведения и формулы (3.20.1) имеем .

Следствие 3.20.2. Для любых векторов справедлива формула Лагранжа

.

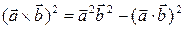Доказательство. .

Дата добавления: 2014-01-05