Вероятность попадания случайной величины на заданный интервал

ФОРМЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ ДЛЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

ФОРМЫ ЗАДАНИЯ ЗАКОНА РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

1). Таблица (ряд)распределения — простейшая форма задания закона распределения дискретных случайных величин.

x	x1	x2	x3	…	xn	xi — возможные значения случайной величины X, pi — соответствующие им вероятности.
P	p1	p2	p3	…	pn

, так как в таблице перечислены все возможные значения случайной величины.

2). Многоугольник распределения. При графическом изображении ряда распределения в прямоугольной системе координат по оси абсцисс откладывают все возможные значения случайной величины, а по оси ординат — соответствующие им вероятности. Затем наносят точки и соединяют их прямолинейными отрезками. Полученная фигура —многоугольник распределения — также является формой задания закона распределения дискретной случайной величины.

3). Функция распределения — вероятность того, что случайная величина Х примет значение, меньшее некоторого заданного х, т.е

.

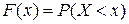С геометрической точки зрения можно рассматривать как вероятность попадания случайной точки Х на участок числовой оси, расположенный левее фиксированной точки х.

Свойства функции распределения:

1) ;

2) ; ;

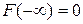3) , если .

Задача 2.1. Случайная величина Х — число попаданий в мишень при 3‑х выстрелах (см. задачу 1.5). Построить ряд распределения, многоугольник распределения, вычислить значения функции распределения и построить её график.

Решение:

1) Ряд распределения случайной величины Х представлен в таблице

x
p	0,34	0,44	0,19	0,03

2) Выбрав произвольно масштаб по осям х и р, строим многоугольник распределения (рис. 2.1).

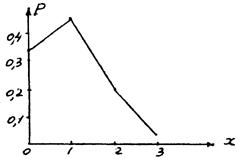
Рис. 2.1 — Многоугольник распределения

3) Функция распределения. Для дискретной величины Х значения функции распределения вычисляют по формуле

.

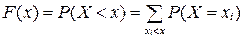Находим:

При	,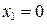
При	,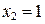
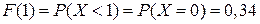При	,
При
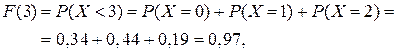
при	.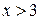

Откладывая по оси абсцисс значения х, а по оси ординат — значения и выбрав определённый масштаб, получим график функции распределения (рис. 2.2). Функция распределения дискретной случайной величины имеет скачки (разрывы) в тех точках, в которых случайная величина Х принимает конкретные значения, указанные в таблице распределения. Сумма всех скачков функции распределения равна единице.

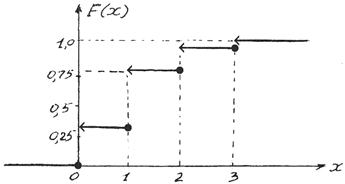
Рис. 2.2 — Функция распределения дискретной величины

1). Функция распределения.

Для непрерывной случайной величины график функции распределения (рис. 2.3) имеет форму плавной кривой.

Свойства функции распределения:

а) ;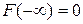

б) ;

в) , если .

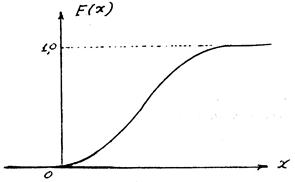
Рис. 2.3 — Функция распределения непрерывной величины

2). Плотность распределения определяется как производная от функции распределения, т.е.

.

Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 2.4).

Свойства плотности:

а) , т.е. плотность есть неотрицательная функция;

б) 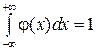, т.е. площадь, ограниченная кривой распределения и осью абсцисс, всегда равна 1.

Если все возможные значения случайной величины Х заключены в пределах от a до b, то второе свойство плотности примет вид:

.

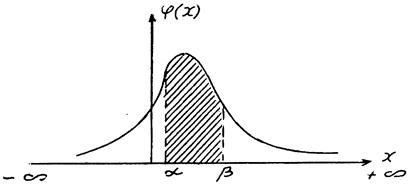
Рис. 2.4 — Кривая распределения

На практике часто оказывается необходимым знать вероятность того, что случайная величина Х примет значение, заключённое в некоторых пределах, например, от a до b. Искомая вероятность для дискретной случайной величины Х определяется по формуле

,

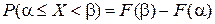при этом условились левую границу a включать в участок , а правую β — не включать.

Для непрерывной случайной величины Х формула примет вид:

,

так как вероятность любого отдельного значения непрерывной случайной величины равна нулю: .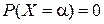

Вероятность попадания непрерывной случайной величины Х на интервал (a,b) определяется также выражением:

.

Эта вероятность численно равна заштрихованной площади на рис. 2.4.

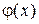Выразим функцию распределения через плотность . Функция распределения определяется выражением, а, учитывая, получаем формулу для вычисления функции распределения непрерывной случайной величины

,

где х в верхнем пределе интегрирования представляет собой конкретное значение аргумента.

Задача 2.2. В условиях задачи 2.1 найти вероятность того, что число попаданий в мишень будет находиться в пределах от 1 до 3 (т.е. будет равно или 1, или 2).

Решение. На основании имеем

.

Действительно,

.

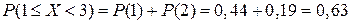Задача 2.3. Случайная величина Х задана функцией распределения

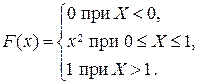
Найти плотность 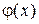, а также вероятность того, что в результате испытания случайная величина Х примет значение, заключённое в интервале .

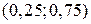Решение:

1.

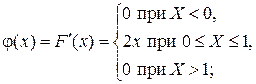
2. Вероятность попадания случайной величины Х в интервал 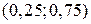определяем по формуле. Принимая 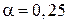и , находим

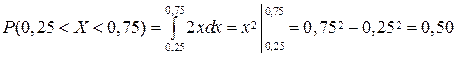
или по формуле

.

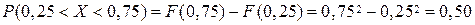Дата добавления: 2014-01-05