Пример. Вертолёт движется поступательно горизонтально и прямолинейно со скоростью V = 50 м/с (180 км/час).Несущий четырёхлопастный винт вертолёта вращается с угловой

Вертолёт движется поступательно горизонтально и прямолинейно со скоростью V = 50 м/с (180 км/час).Несущий четырёхлопастный винт вертолёта вращается с угловой скоростью w = 20 с^-1 (» 200 об/мин). Длина лопастей винта = 6 м.

Определить абсолютные скорости точек на концах лопастей винта, когда две лопасти расположены вдоль продольной оси вертолёта, а две – перпендикулярны к ней.

РЕШЕНИЕ. Абсолютное движение точек A, B, C, D – движение относительно земли (неподвижного воздуха).

Относительное движение этих точек – вращение вместе с винтом относительно корпуса вертолёта, относительные траектории – окружности с центром в точке О и радиуса .

Переносное движение точек – поступательное движение вместе с вертолётом, переносные траектории – прямые линии.

В соответствие с изложенным находим модули относительных скоростей точек (для всех точек одинаковых)

м/с

и изображаем векторы этих скоростей

Так как переносное движение поступательное, то переносные скорости всех точек равны скорости вертолёта

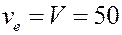м/с.

Согласно формуле (4) сложения скоростей точки при сложном движении изображаем векторы абсолютных скоростей точек

Учитывая взаимное расположение векторов скоростей, находим модули абсолютных скоростей точек.

Для точек А и С:

м/с.

Для точки В: м/с.

Для точки D: м/с.

Таким образом, при движении вертолёта абсолютные скорости точек несущего винта изменяются от 70 до 170 м/с.

2.Сложение ускорений точки при сложном движении (кинематическая теорема Кориолиса).

По определению

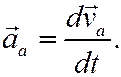
Учитывая, что абсолютная скорость точки определена равенством (2), подставим его в формулу для и вычислим производную по всем правилам дифференцирования. Тогда

По определению

абсолютное ускорение точки «о» начала подвижной системы координат (абсолютная производная от абсолютного вектора). Далее

угловое ускорение подвижной системы координат (производная от угловой скорости не зависит от системы координат).

Векторы и заданы в подвижной системе координат, а надо вычислить абсолютные производные. Применяем формулу Бура:

В силу этих выражений последнее слагаемое в равенстве для абсолютного ускорения запишется

Учитывая, что

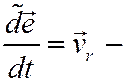
относительная скорость точки, а

относительное ускорение точки (по определению), и подставляя все полученные выражения в формулу для , получим после перегруппировки слагаемых

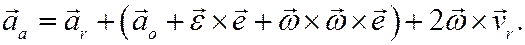
По определению выражение в скобках

это переносное ускорение точки (ускорение полюса «о» плюс ускорение точки при вращении вокруг полюса при постоянном модуле вектора ).

Кроме того, в выражении для появилось третье слагаемое

которое зависит от угловой скорости вращения подвижной системы координат и от относительной скорости точки и называется поворотным, или кориолисовым ускорением точки. Это ускорение будет подробно рассмотрено позже.

С учётом вышесказанного можем окончательно записать

т.е. абсолютное ускорение точки равно сумме трёх ускорений: относительного, переносного и кориолисова (кинематическая теорема Кориолиса).

Частные случаи переносного движения.

1) Переносное движение – поступательное. В этом случае 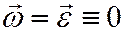и из формул (8) и (9) следует

Следовательно, формула сложения ускорений (10) превращается в

Объяснение такое же, как и в случае скорости: при поступательном движении подвижной системы координат, как твёрдого тела, относительно неподвижной ускорения всех связанных с ней точек в любой момент времени равны между собой и равны ускорению начала «о».

2) Переносное движение – вращательное. Аналогично сложению скоростей, начало «о» выбираем на оси вращения. Тогда составляющие переносного ускорения и определяются как при вращательном движении тела. Следовательно, при переносном вращательном движении можем записать:

Модули и направления этих составляющих находятся так же, как и при вращательном движении тела; следует только определять расстояние от текущего положения точки М до оси вращения.

Кориолисово ускорение в этом случае находится по общей формуле (9).

В остальных случаях переносного движения (плоскопараллельном, сферическом и свободном) переносное и кориолисово ускорения находятся по общим формулам (8), (9).

3. Ускорение Кориолиса.

Вектор находится по формуле (9):

Модуль ускорения равен

Из равенства (13) следует, что ускорение Кориолиса равно нулю в трёх случаях:

1) (подвижная система движется либо поступательно, либо в данный момент не вращается);

2) (точка покоится в подвижной системе координат);

3) (в подвижной системе координат точка движется параллельно оси вращения системы).

Направление вектора ускорения Кориолиса определяется либо по общему для векторных произведений правилу (перпендикулярно плоскости туда, откуда поворот первого сомножителя ко второму на наименьший угол происходит против хода часовой стрелки), либо по правилу Н.Е.Жуковского.

Правило Жуковского для определения направления кориолисова ускорения.

Для определения направления ускорения Кориолиса надо:

1) выбрать плоскость, перпендикулярную к оси переносного вращения;

2) спроектировать вектор относительной скорости на выбранную плоскость;

3) повернуть полученную проекцию на угол 90° по направлению переносного вращения.

Полученное направление и будет направлением кориолисова ускорения. В этом направлении следует отложить вычисленный ранее по формуле (13) модуль ускорения.

В некоторых практических задачах применение правила Жуковского упрощается: вектор относительной скорости точки сразу расположен в плоскости, перпендикулярной к оси переносного вращения. Тогда для определения направления ускорения Кориолиса надо просто повернуть вектор относительной скорости на угол 90° по направлению переносного вращения. Примеры.

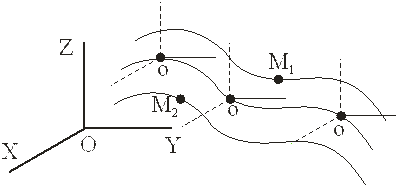
Более сложный пример: движение точки по поверхности Земли с севера на юг вдоль меридиана.

В северном полушарии кориолисово ускорение точки будет направлено к востоку. В момент пересечения точкой экватора ускорение Кориолиса обратится в нуль (вектор относительной скорости параллелен оси вращения Земли). При движении с севера на юг в южном полушарии кориолисово ускорение направлено к западу.

Физический смысл кориолисова ускорения: согласно равенству (9) ускорение Кориолиса состоит из двух слагаемых.

Первое слагаемое определяет изменение относительной скорости за счёт переносного движения точки. Действительно

Второе слагаемое определяет изменение переносной скорости за счёт относительного движения точки.

Согласно равенству (10) абсолютное ускорение точки в общем случае равно сумме трёх ускорений. Поэтому для определения модуля абсолютного ускорения следует использовать общий приём: выбрать какую-либо систему координат, спроектировать формулу (10) на эти оси и найти проекции абсолютного ускорения

Тогда модуль ускорения будет равен

Рассмотрим примеры.

Пример 1. Прямоугольная пластина прикреплена шарнирами в точках А и В к двум одинаковым кривошипам длины r = 10 см. Кривошипы вращаются вокруг осей О₁ и О₂ по закону рад. По каналу CD пластины движется груз М по закону см.

В момент, когда кривошипы наклонены к горизонтали на угол 60°, найти абсолютные скорость и ускорение груза.

Решение. Относительное движение груза – движение по пластинке. Относительная траектория – прямая CD. – это закон относительного движения (относительное движение задано естественным способом: траектория, начало отсчёта, положительное направление и закон движения по траектории).

Переносное движение – движение вместе с пластиной. Пластина движется поступательно, т.к. кривошипы одинаковы. Следовательно, переносное движение – поступательное. Переносные траектории – окружности радиуса r.

Абсолютное движение – движение груза относительно неподвижной плоскости, связанной с основаниями кривошипов. Абсолютные траектории – сложные кривые.

Примеры абсолютных траекторий.

Так как переносное движение поступательное (), то, выбирая в качестве полюса «о» точку В, будем искать абсолютные скорость и ускорение согласно равенствам

Относительная скорость

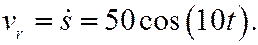
Относительное ускорение

Легко установить, что, когда кривошипы составляют с горизонталью угол , момент времени t будет равен .

Тогда при получим

см/с.

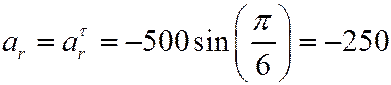см/с².

Знаки показывают, что вектор направлен от центра О (в сторону возрастания s), а вектор – к точке О (модуль относительной скорости уменьшается).

Так как переносное движение поступательное, то переносными скоростью и ускорением точки М будут скорость и ускорение точки В пластины. Находим угловую скорость и угловое ускорение кривошипа (не путать с угловыми скоростью и ускорением пластины – они равны 0!)

Модуль скорости точки В

см/с.

Модуль ускорения точки В

Модули не зависят от времени. Так как , то кривошипы вращаются против часовой стрелки (в сторону возрастания угла ).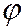

В результате получаем картинки.

С помощью этих рисунков можем получить

Аналогичные результаты можно получить, если воспользоваться «универсальным» способом. Выберем координатные оси: ось x – горизонтально вправо; ось y – вертикально вверх. Тогда

Для ускорения получим

Пример 2. Круглая пластина радиуса R = 20 см вращается вокруг оси О, перпендикулярной плоскости пластины и расположенной на её краю, по закону рад. По краю пластины, начиная от точки О, движется груз по закону см.

В момент времени t = 1 с найти абсолютные скорость и ускорение груза.

Решение. Относительное движен ие – движение по краю пластины. Относительная траектория – окружность радиуса R с центром в О₁. s(t) – это закон относительного движения. Относительное движение задано, таким образом, естественным способом.

Переносное движение – это вращение вместе с пластиной по закону , т.е. переносное движение вращательное. Переносные траектории – окружности с центрами в точке О.

Абсолютное движение – движение относительно неподвижной плоскости, связанной с основанием шарнира О. Абсолютные траектории – сложные кривые, зависящие от законов движения s и j. Рассмотрим ряд примеров абсолютного движения для заданных в условии задачи законов, а также для

Находим положение груза на пластине при t = 1 с: s(1) = 10p см, что составляет четверть длины окружности пластины (2pR = 40p см). Положение можно также установить, вычислив центральный угол: q = s(1)/R = p/2 рад.

Следовательно, при t = 1 с переносной траекторией груза будет окружность с центром в О и радиуса см.

Находим относительную скорость: т.к. относительное движение задано естественным способом, то

см//с.

Для определения переносной скорости найдём угловую скорость пластины (переносную угловую скорость)

Тогда

см/с.

Изображаем векторы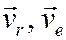

и,согласно равенству , – вектор абсолютной скорости. Из рисунка следует

Через проекции на оси O₁xy:

Тогда

Определяем относительное ускорение:

Находим переносное ускорение точки: угловое ускорение пластины равно

Тогда

Определяем модуль кориолисова ускорения

Изображаем направления всех векторов на рисунке:

Согласно формуле

находим абсолютное ускорение груза: вычисляем проекции вектора на оси координат

Тогда

см/с².

Дата добавления: 2014-01-05