Лекция 3

Теорема об изменении количества движения системы.

Кинетический момент системы.

Вопросы лекции.

1. Количество движения точки и системы, импульс силы.

2. Теорема об изменении количества движения системы. Закон сохранения количества движения.

3. Момент количества движения точки и кинетический момент системы и твёрдого тела.

4. Понятие о моментах инерции твёрдых тел, их вычисление.

Тарг, 2009, с. 265 – 269, 280 – 284, 290 – 291.

1. Количество движения точки и системы, импульс силы.

Пусть точка массы m движется в заданной системе координат по закону

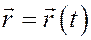
и имеет в данный момент времени скорость

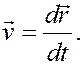
Тогда

количеством движения точки называется вектор, равный произведению массы точки на её скорость:

Согласно (3) вектор количества движения направлен вдоль скорости, т.е. по касательной к траектории точки, а модуль количества движения отличается от модуля скорости только скалярным множителем – массой точки m. Поэтому проекции количества движения точки на оси декартовой системы координат Oxyz определятся согласно равенствам:

а модуль

Переходим теперь к движению механической системы.

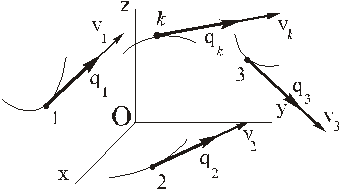
Для каждой точки системы по формуле (3) считаем вектор количества движения

переносим параллельно полученные векторы в центр О и складываем. Получаем вектор

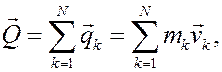
называемый

главным вектором количеств движения системы,

или, просто,

количеством движения системы.

Согласно выражениям (4) и (5) можно найти проекции на оси и модуль количества движения системы.

Но если вспомнить формулу (21) прошлой лекции:

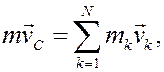
то равенство (6) можно записать так

т.е. количество движения системы можно вычислять как произведение массы всей системы на скорость её центра масс.

Таким образом, при любом движении твёрдого тела

его количество движения определится по формуле (7). В частности, при любом качении однородного колеса (со скольжением, или, без скольжения) по плоскости его количество движения равно произведению массы колеса на скорость его центра.

Если тело совершает вращательное движение

то

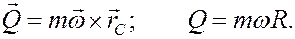
Отсюда следует, что если центр масс вращающегося тела находится на оси вращения

то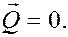

Рассмотрим движение точки под действием силы .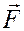

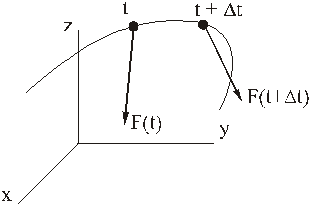
Произведение

называют средним импульсом силы за промежуток времени 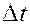. Если в этом равенстве перейти к пределу при , то получим величину

называемую элементарным импульсом силы.

Если точка под действием силы движется из положения М₀ в положение М₁

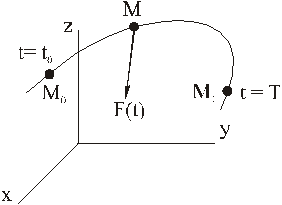
то, разбивая траекторию на малые участки, вычисляя на каждом из них средние импульсы и складывая, получим

и, переходя к пределу при , получим вектор

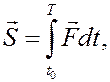
называемый импульсом силы за промежуток времени , или, просто, – импульсом силы.

Согласно (9) для определения проекций импульса силы на какие-либо оси нужно вычислять интегралы от соответствующих проекций силы

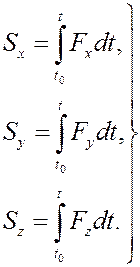
Затем может быть найден модуль импульса

Рассмотрим примеры.

1) Вектор силы, действующей на точку, определён равенством

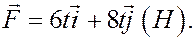
Вычислить импульс этой силы за промежуток времени от 0 до 2 с и найти модуль этого импульса.

РЕШЕНИЕ. По формуле (9) получаем

Таким образом, . Поэтому

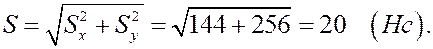
Можно было бы сразу найти 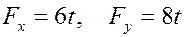, а затем по формулам (10) вычислить

Тогда .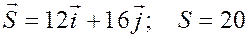

2) проекция на ось x силы, действующей на точку, задается равенством

Найти проекцию импульса силы на ось x за промежуток от 0 до с.

РЕШЕНИЕ. По первой из формул (10) получим

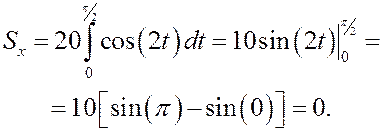
2. Теорема об изменении количества движения системы. Закон сохранения количества движения.

Запишем дифференциальное уравнение движения центра масс

Считая, что массы всех точек системы постоянны и, следовательно, , внесём массу системы под знак дифференциала

Но согласно (7)

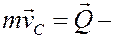
это количество движения системы. Следовательно,

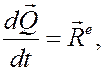
т.е. производная по времени от количества движения системы равна главному вектору всех внешних сил, действующих на систему.

Это и есть теорема об изменении количества движения системы в дифференциальной форме, а равенство (12) – её математическое выражение.

В проекциях на оси Oxyz уравнение (12) записывается очевидным образом

На практике теорему об изменении количества движения чаще применяют в интегральной форме. Чтобы её получить, равенство (12), домножив обе части на , перепишем в виде

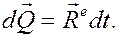
От обеих частей полученного равенства вычислим интегралы на промежутке времени от 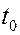до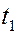

Левый интеграл – это просто разность значений количеств движения в конечный и начальный моменты времени:

Справа же получаем

т.е. сумму импульсов всех внешних сил, действующих на систему.

Окончательно:

Равенство (14) выражает теорему об изменении количества движения системы в интегральной форме:

изменение количества движения системы за любой конечный промежуток времени равно сумме импульсов всех внешних сил за этот промежуток времени.

В проекциях на оси Oxyz получим

Пусть для какого-либо промежутка времени оказывается, что

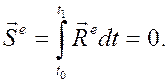
Тогда из (14) будет следовать, что

т.е. количество движения системы за этот промежуток времени не изменится. Это и есть закон сохранения количества движения системы:

если за какой-либо промежуток времени импульс всех внешних сил равен нулю, то количество движения системы за этот промежуток времени не изменяется.

В частном случае может быть

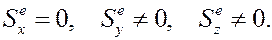
Тогда из первого равенства (15) получим

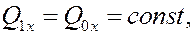
а проекции количества движения на оси y и z изменяются в соответствие со вторым и третьим равенствами (15).

3. Момент количества движения точки и кинетический момент системы и твёрдого тела.

Пусть точка массы m движется по закону в какой-либо системе отсчёта. Вычисляем скорость этой точки

находим количество движения точки

и определяем момент этого вектора 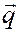относительно центра О:

Полученный вектор называется моментом количества движения точки относительно центра О.

Если сравнить равенство (18) с выражением для момента силы относительно центра О

то легко установить, что вектор момента количества движения точки имеет такие же свойства и вычисляется по тем же правилам, что и момент силы: нужно только вместо вектора силы брать вектор количества движения точки .

Отсюда следует:

вектор

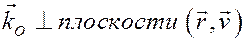
и направлен так, что с его конца вращение точки происходит против хода часовой стрелки;

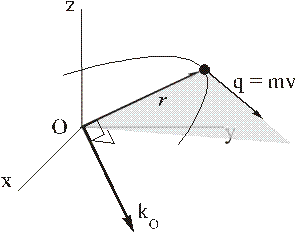
модуль вектора равен

где h – плечо вектора : перпендикуляр, опущенный из центра О на касательную к траектории точки.

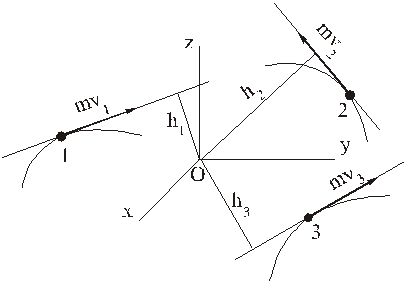
Аналогичным образом вычисляются проекции момента количества движения на оси координат.

Момент силы. Момент количества движения.

Переходим к механической системе. Пусть система состоит из N точек с массами . Положение точек определено с помощью радиус-векторов .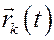

Определяем скорости точек системы

находим количества движения

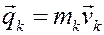
и определяем согласно (18) моменты количеств движения всех точек относительно центра О

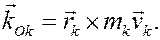
Затем все полученные векторы складываем и получаем вектор, равный

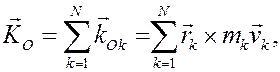
и называемый главным моментом количеств движения механической системы, или, кинетическим моментом системы.

Вычисляется кинетический момент системы по проекциям на оси координат:

Модуль кинетического момента найдётся после этого по известной формуле

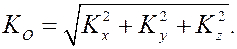
Рассмотрим пример. Твёрдое тело вращается вокруг неподвижной оси АВ с угловой скоростью .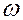

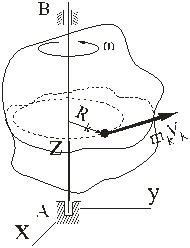
Определить проекцию кинетического момента этого тела на ось вращения.

Направим вдоль оси вращения координатную ось z. Для определения проекции кинетического момента на ось z воспользуемся третьим выражением (21). Имеем из кинематики

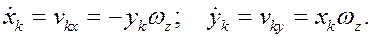
Подставив эти равенства в (21), получим

Выражение

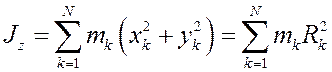
называется осевым моментом инерции тела.

Окончательно, таким образом, получаем

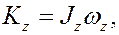
т.е. проекция кинетического момента вращающегося твёрдого тела на ось вращения равна произведению момента инерции тела на его угловую скорость.

В формулу (24) входит величина, определённая равенством (23) и называемая осевым моментом инерции тела. Моменты инерции в дальнейшем будут необходимы очень часто, поэтому прежде чем двигаться дальше рассмотрим вопрос о моментах инерции более подробно.

4. Понятие о моментах инерции твёрдых тел, их вычисление.

Моменты инерции – это величины, характеризующие распределение массы по объёму, занимаемому твердым телом.

Моменты инерции бывают полярными, осевыми и центробежными. Подробно будут рассмотрены лишь осевые моменты инерции.

Рассмотрим механическую систему (или твёрдое тело) и проведём какую-либо ось .

Обозначая через 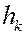расстояние от проведённой оси до точки с массой , введём величину

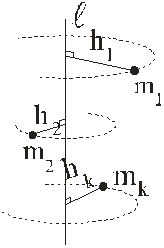
равную сумме произведений масс всех точек системы на квадраты их расстояний до оси.

Эта введённая величина и называется осевым моментом инерции системы.

Из определения (25) видно, что

и обращается в нуль только, если все точки системы лежат на оси . Размерность момента инерции согласно (25) в систем СИ .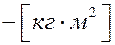

Осевой момент инерции характеризует распределение массы системы относительно оси: если все точки отодвинуть от оси, в два раза увеличив расстояния, то согласно (25) момент инерции увеличится в четыре раза и т.п.

На практике чаще требуется определять моменты инерции не относительно произвольной оси, а относительно координатных осей 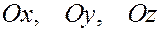. Если положения точек системы заданы координатами 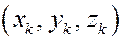, то из (25) следует

Совершенно аналогично для двух других координатных осей получим:

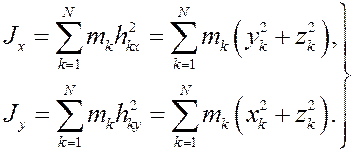
Т.к. согласно (25) моменты инерции суть неотрицательные величины, то их можно записать в виде

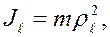
где 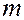– масса всей системы (или тела), а 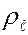– радиус инерции системы (или тела) относительно оси. Из (28) сразу виден физический смысл радиуса инерции:

радиус инерции системы – это такое расстояние от оси, на котором нужно сосредоточить всю массу системы, чтобы момент инерции полученной точки относительно оси был равен моменту инерции системы.

Из (28) следует

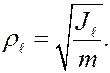
При вычислении моментов инерции твёрдых тел вместо сумм во всех формулах следует вычислять интегралы по объёму тела

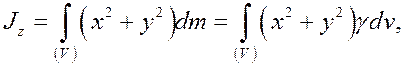
где 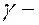плотность тела в данной точке. Поэтому вычисление моментов инерции произвольных тел представляет достаточно сложную задачу. Для часто встречающихся на практике тел (шары, конусы, параллелепипеды, цилиндры и пр.) моменты инерции относительно центральных осей (т.е. осей, проходящих через центр масс тела) приводятся в справочниках. Для простейших однородных тел моменты инерции могут быть непосредственно вычислены по приведенной выше формуле.

Запишем без вывода моменты инерции некоторых простейших тел, с которыми будем иметь дело на практике.

1) Тонкое однородное кольцо массы m и радиуса R.

2) Тонкий однородный диск массы m и радиуса R.

Дата добавления: 2014-01-05