Группы, их основные свойства и типы

Дадим независимое определение группы.

Определение 3.2.1. Группой называется непустое множество G с определенной на нем бинарной алгебраической операцией ·, которая обладает свойствами:

1) ассоциативность – (a · b)· c = a ·(b · c) для любых a, b, c Î G;

2) существует нейтральный элемент, то есть такой элемент e Î G, что g · e = e · g = g для каждого g Î G;

3) каждый элемент g Î G имеет обратный, то есть такой элемент h Î G, что g · h = h · g = e.

В любой группе нейтральный элемент и обратный к каждому элементу единственны в силу их определений и ассоциативности операции. Знак групповой операции ·, как и знак умножения, можно в записи опускать.

Определение 3.2.2. Абелевой (Нильс Абель (1802–1829) – норвежский математик) или коммутативной называется группа (G, ·) со свойством a · b = b · a для произвольных a, b Î G, в противном случае группа называется неабелевой или некоммутативной.

Определение 3.2.3. Группа относительно операции сложения называется аддитивной группой. Исторически так сложилось, что все аддитивные группы абелевы. Нейтральный элемент аддитивной группы называют нулем и обозначают символом 0, а обратный элемент к элементу a – противоположным и обозначают – a.

Пример 3.2.1. Аддитивные группы: (Z, +), (Q, +), (R, +), (C, +), (Z / n Z, +) для " n Î N. ·

Пример 3.2.2. Пусть K – одно из множеств: Z, Q, R, C или Z / k Z для " k Î N. К аддитивным относятся группы (M_{m ´ n} (K), +) – множество прямоугольных матриц порядка m ´ n (m, n Î N – произвольные фиксированные числа) с коэффициентами из множества K относительно операции сложения матриц и (V_n (K), +) – множество n -мерных векторов с компонентами из множества K относительно операции векторного сложения (n Î N – произвольное фиксированное число). ·

Определение 3.2.4. Группа относительно операции умножения называется мультипликативной группой. Нейтральный элемент мультипликативной группы называют единицей и часто обозначают символом 1, а обратный элемент к элементу a обозначают a ^–1.

Пример 3.2.3. Примерами абелевых мультипликативных групп являются (Q ^*, ×), (R ^*, ×), (C ^*, ×), ({–1, 1}, ×), (Z / n Z ^*, ×) для " n Î N. ·

Пример 3.2.4. Пусть K – одно из множеств: Q, R или C. Полной линейной группой GL_n (K) (от англ. general linear group – «полная линейная группа») называется множество всех квадратных матриц порядка n Î N с коэффициентами из K и ненулевым определителем с операцией матричного умножения. GL_n (K) является неабелевой мультипликативной группой при 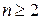, так как произведение матриц не коммутативно в общем случае. ·

Определение 3.2.5. Группа (G, ·) называется конечной, если G – конечное множество, в противном случае – бесконечной. Порядком конечной группы | G | называется мощность множества G.

Алгебраическая операция в конечной группе может быть задана таблицей Кэли.

Пример 3.2.5. Конечными являются группы: (Z / n Z, +) порядка n, (Z / n Z ^*, ×) порядка 1 при n = 1 и порядка j (n) при 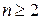, (M_{m ´ n} (Z / k Z), +) порядка k^mn, (V_n (Z / k Z), +) порядка kⁿ. Бесконечные группы: (K, +), (M_{m ´ n} (K), +), (V_n (K), +), где K – одно из множеств: Z, Q, R или C, а также (K ^*, ×) и GL_n (K), где K – одно из множеств: Q, R или C. ·

Для каждого n Î N существуют абелевы аддитивная и мультипликативная группы порядка n. Примерами таких групп являются (Z / n Z, +) и C_n – мультипликативная группа всех комплексных корней n -ой степени из 1, то есть чисел , в частности С ₂ = ({–1, 1}, ×).

Дата добавления: 2014-01-05