Численное решение линейных дифференциальных уравнений

Рассмотрим уравнение вида

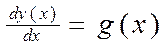, (5.11)

где y(x) – неизвестная функция; g(x) – заданная функция.

Уравнение вида (5.11) называют дифференциальным уравнением первого порядка, поскольку в него входит только первая производная неизвестной функции y=y(x).

В общем случае аналитического решения уравнения (5.11) не существует. Кроме того, даже если аналитическое решение существует, часто бывает необходимо его представить в графическом виде, чтобы понять его характер. Эти причины побуждают искать не точные, а приближенные численные решения дифференциальных уравнений.

Типичный метод численного решения дифференциальных уравнения включает в себя преобразование дифференциального уравнения в алгебраическое разностное. Пусть нам необходимо найти решение уравнения (5.11) в точке x=x_k. Положим, что при x=x₀ функция y(x) принимает значение y₀. Разобьем интервал (x₀,x_k) на n интервалов шириной Dx. Поскольку уравнение (5.11) описывает скорость изменения функции y(x) в точке x₀, то можно найти приближенное значение функции y в близлежащей точке x₁=x₀+Dx, если Dx мало. Будем считать в первом приближении, что функция g(x) постоянна на отрезке (x₀,x₁). В этом случае приближенное значение y(x₁) определяется выражением

y(x₁)=y₁»y(x₀)+Dy=y(x₀)+g(x₀)*Dx.

Определив y₁, мы можем повторить эту процедуру и найти значение y в точке x₂=x₁+Dx:

y(x₂)=y₂»y(x₁)+Dy=y(x₁)+g(x₁)*Dx.

Очевидным образом это правило можно обобщить и вычислить значение функции в любой точке x_i=x_i-1+Dx, в том числе в интересующей нас точке x_n=x_k по итерационной формуле

y(x_i)=y_i»y(x_i-1)+Dy=y(x_i-1)+g(xi-₁)*Dx, i=1, 2…n. (5.12)

Итак, выполнив n шагов вычислений по формуле (5.12), мы получаем решение уравнения (5.11).

Задание

Используя метод Эйлера, решите численно дифференциальное уравнение dy/dx=2x в точке x=2 c начальными условиями x₀=1, y₀=1.

Выберите шаг Dx=0.1. Вычислив приближенное решение y(x), сравните его с точным решением уравнения и вычислите относительную ошибку.

Дата добавления: 2014-01-05