
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П а р а б о л а
|
|
|
|
Отрезок, соединяющий точки и называется мнимой осью гиперболы. Его длина равна 2b. Число b- мнимой полуосью.Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы.
Из канонического уравнения гиперболы следует, что  или
или 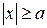 . Это означает, что точки гиперболы расположены слева от прямой
. Это означает, что точки гиперболы расположены слева от прямой  (правая ветвь гиперболы) и слева от прямой
(правая ветвь гиперболы) и слева от прямой 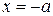 (левая ветвь гиперболы). Из уравнения гиперболы видно, что когда
(левая ветвь гиперболы). Из уравнения гиперболы видно, что когда  возрастает, то и
возрастает, то и  возрастает. Значит, гипербола имеет форму, изображенную на рисунке и состоит из двух не связанных между собой частей, называемых ее ветвями.
возрастает. Значит, гипербола имеет форму, изображенную на рисунке и состоит из двух не связанных между собой частей, называемых ее ветвями.
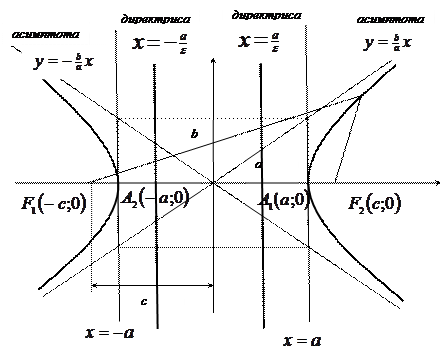
| О(0;0)центр гиперболы;
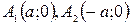 вершины гиперболы; вершины гиперболы;
 действительная ось гиперболы, действительная ось гиперболы,
 мнимая ось гиперболы;
мнимая ось гиперболы;
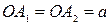 - действительная полуось гиперболы, - действительная полуось гиперболы,
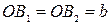 мнимая ось гиперболы;
Эксцентриситет гиперболы
мнимая ось гиперболы;
Эксцентриситет гиперболы  Асимптоты гиперболы
Асимптоты гиперболы Директрисы гиперболы
Директрисы гиперболы  . .
|
Асимптота: Прямая L называется асимптотой неограниченной кривой К, если расстояние d от точки М кривой К до этой прямой стремится к нулю при неограниченном удалении точки М вдоль кривой К от начала координат.
Гипербола имеет две асимптоты, уравнения которых 
При построении гиперболы целесообразно сначала построить основной прямоугольник гиперболы, провести прямые, проходящие через противоположные вершины этого прямоугольника, - асимптоты гиперболы и отметить вершины гиперболы.
Отношение  называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
С учетом того, что с2 – а2 = b2:
 ,
,  .
.
Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение 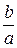 ее полуосей, а значит, тем более вытянут ее основной прямоугольник.
ее полуосей, а значит, тем более вытянут ее основной прямоугольник.
Гипербола называется равносторонней, если ее полуоси равны (а=b). Ее каноническое уравнение 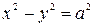 . Асимптоты равносторонней гиперболы имеют уравнения
. Асимптоты равносторонней гиперболы имеют уравнения  и
и  и, следовательно, являются биссектрисами координатных углов. Уравнение равносторонней гиперболы, для которой оси Ох, Оу являются асимптотами, будет иметь вид
и, следовательно, являются биссектрисами координатных углов. Уравнение равносторонней гиперболы, для которой оси Ох, Оу являются асимптотами, будет иметь вид 
|
|
|
Эксцентриситет равносторонней гиперболы равен 

Фокальные радиусы 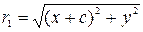 и
и 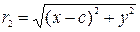 для точек правой ветви гиперболы имеют вид
для точек правой ветви гиперболы имеют вид 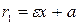 и
и  , а для левой -
, а для левой - 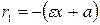 и
и 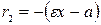 .
.
Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии 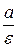 от него, называются директрисами гиперболы. Их уравнения:
от него, называются директрисами гиперболы. Их уравнения:  .
.
Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.
Кривая, определяемая уравнением 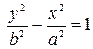 , также есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось на оси Ох. Очевидно, что гиперболы
, также есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось на оси Ох. Очевидно, что гиперболы 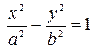 и
и 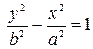 имеют общие асимптоты. Такие гиперболы называются сопряженными.
имеют общие асимптоты. Такие гиперболы называются сопряженными.

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.
Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы – буквой р и называется фокальным параметром параболы.
Выведем уравнение параболы. Для этого расположим систему координат так, чтобы ось абсцисс проходила через фокус F перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посредине между фокусом и директрисой.
В выбранной системе координат фокус F имеет координаты 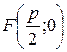 , а директриса имеет уравнение
, а директриса имеет уравнение 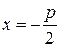 или
или 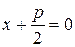 .
.
Пусть M(x,y) - произвольная точка параболы. Опустим из точки М перпендикуляр на директрису, и пусть N – основание этого перпендикуляра. Длина отрезка MN равна расстоянию от точки М до директрисы. Расстояние от точки М до фокуса равно длине отрезка MF. Тогда координаты точек параболы удовлетворяют уравнению
|
|
|
 .
.
Возведем обе части уравнения в квадрат и приведем подобные члены:
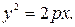
Уравнение  называется каноническим уравнением параболы.
называется каноническим уравнением параболы.

Из уравнения  следует, что парабола симметрична относительно оси Ох; ось Ох является осью симметрии параболы.
следует, что парабола симметрична относительно оси Ох; ось Ох является осью симметрии параболы.
Так как р>0, то следовательно  и парабола расположена справа от оси Оу.
и парабола расположена справа от оси Оу.
При х=0 имеем у=0. Значит, парабола проходит через начало координат.
При неограниченном возрастании х модуль у также неограниченно возрастает. Парабола имеет вид, изображенный на рисунке. Точка О(0;0) называется вершиной параболы, отрезок FM называется фокальным радиусом точки М.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат с вершиной, то парабола лежит в левой полуплоскости и ее уравнение имеет вид  . .
| 
|
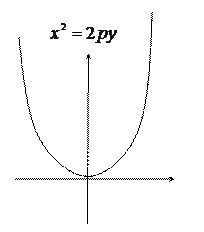
| В случае, когда начало координат находится в вершине, а ось совмещена с осью ординат, парабола будет иметь уравнение  , если она лежит в верхней полуплоскости. , если она лежит в верхней полуплоскости.
|
В случае, когда начало координат находится в вершине, а ось совмещена с осью ординат, парабола будет иметь уравнение  , если она лежит в нижней полуплоскости. , если она лежит в нижней полуплоскости.
| 
|
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 431; Нарушение авторских прав?; Мы поможем в написании вашей работы!