Локальные экстремумы функции двух переменных

Определение. Точка 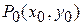называется точкой локального максимума (минимума) функции 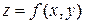, если существует 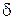-окрестность этой точки, такая, что для всех точек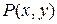 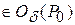(принадлежащих 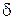-окрестности этой точки), отличных от точки 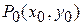, выполняется неравенство ( ).

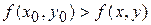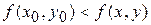Значение 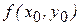называют локальным максимумом (минимумом) функции и пишут

().

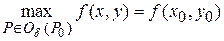Точки максимума и минимума функции называют точками экстремума функции, а максимумы и минимумы функции — экстремумами функции.

Пример. Функция имеет локальный максимум в точке (1; 1): 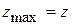(1, 1) = 1.

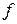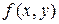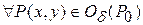Действительно, существует окрестность точки (1; 1), в которой выполняется условие (1; 1) > для . Графиком этой функции является поверхность — параболоид вращения, представленный на рисунке.

Отметим, что если функция 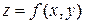имеет в точке 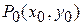локальный экстремум, то:

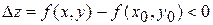в случае локального максимума,

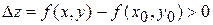в случае локального минимума.

Из сказанного выше следует, что полное приращение функции не меняет знака в . Однако для всех точек 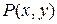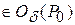определить знак приращения практически невозможно, поэтому надо искать другие условия, по которым можно судить о наличии и характере экстремума функции в данной точке.

Теорема (необходимые условия существования локального экстремума). Если в точке 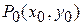дифференцируемая функция 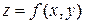имеет локальный экстремум, то ее частные производные в этой точке равны нулю:

и ,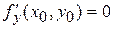

или, по крайней мере, одна из них не существует.

Доказательство. Докажем только первое утверждение теоремы.

Рассмотрим в лишь те точки, для которых 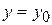. Получим функцию 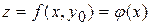одной переменной 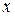. Эта функция имеет в точке 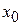экстремум, следовательно, .

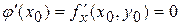Аналогично доказывается, что .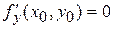

Теорема доказана.

Проиллюстрируем примером второе утверждение теоремы.

Функция имеет максимум в точке О(0; 0; 0), так как для любой точки 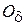(О) выполняется условие 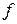(0; 0) > 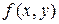. Частные производные

,

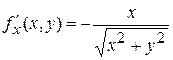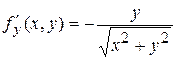
в точке О(0; 0) не существуют для 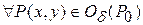. Графиком этой функции является конус, представленный на рисунке.

Следствие. Если функция 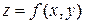имеет в точке 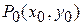локальный экстремум, то ее дифференциал в этой точке равен нулю или не существует.

Точка 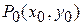, в которой частные производные равны нулю, или хотя бы одна из них не существует, называется точкой возможного экстремума. Такие точки называются также стационарными или критическими.

Равенство нулю частных производных первого порядка не является достаточным условием существования экстремума функции 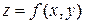в точке .

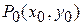Действительно, возьмем, например, функцию 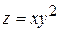. Она задана на всей числовой плоскости R². Точка О(0; 0) будет критической, поскольку частные производные в ней равны нулю. Так как функция равна нулю в точке О, а в любой сколь угодно малой окрестности 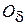(О) она принимает как положительные, так и отрицательные значения, то функция 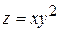не имеет в точке О экстремума.

Теорема (достаточные условия существования локального экстремума). Пусть 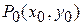— стационарная точка трижды дифференцируемой в функции 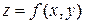и пусть

.

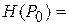
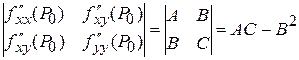Тогда стационарная точка 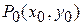является:

1) точкой локального максимума, есл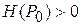и и ;

2) точкой локального минимума, есл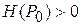и и ;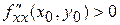

3) если 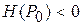, то стационарная точка не является точкой локального экстремума функции.

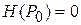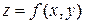Замечание. Если , то нельзя определенно ответить на вопрос о существовании экстремума в точке . В этом случае необходимо произвести дополнительные исследования знака функции в .

Приращения 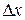и 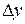не могут равняться нулю одновременно, поскольку в подобном случае точка 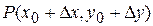совпала бы с точкой и функция 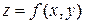не получила бы никакого приращения.

Пример. Исследовать на экстремум функцию .

Решение. Вычислим частные производные первого порядка данной функции:

, .

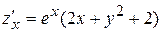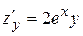Находим точки возможного экстремума. Для этого решим систему уравнений:

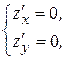
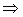
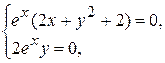
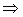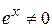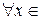(т. к. для R)

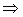
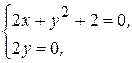
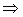
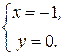
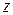Таким образом, существует только одна стационарная точка (-1; 0), в которой функция может достигать экстремума.

Воспользуемся теоремой о достаточных условиях существования локального экстремума.

Для этого найдем частные производные второго порядка функции z:

, , .

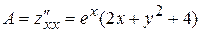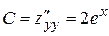Вычислим значения частных производных второго порядка для стационарной точки :

, , .

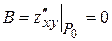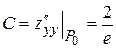Так как (-1; 0) ,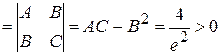

то по теореме о достаточных условиях существования локального экстремума точка (-1; 0) является точкой локального экстремума, а т. к. А > 0, то точка (-1; 0) является точкой локального минимума, при этом

.

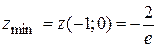Пример. Исследовать на экстремум функцию .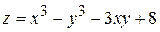

Решение. Вычислим частные производные первого порядка данной функции: , .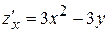

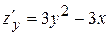Для определения точек возможного экстремума решим систему уравнений:

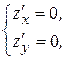
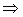
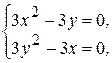
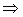
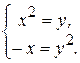
Данная система имеет два решения

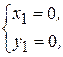и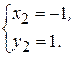

Следовательно, функция имеет две стационарные точки 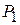(0; 0) и (-1, 1). Вычислим частные производные второго порядка функции :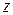

, , .

.

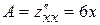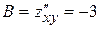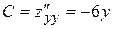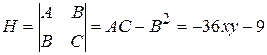Вычислим для точки 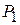(0; 0). Так как (0; 0) 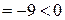, то в точке 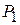(0; 0) нет экстремума.

Вычислим для точки (-1, 1). Т. к. (-1; 1) , то точка (-1, 1) является точкой локального экстремума, а т. к. 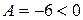, то точка (-1, 1) является точкой локального максимума, при этом

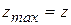(-1; 1)=9.

Пример. Исследовать на экстремум функцию .

Решение. Вычислим частные производные первого порядка функции :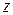

.

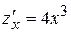
Решая систему уравнений:

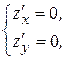
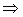
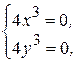
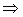
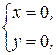
находим единственную стационарную точку (0; 0) данной функции.

Найдем частные производные второго порядка функции :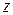

, ,

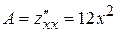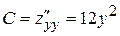
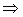
Для стационарной точки (0; 0)

, ,

.

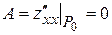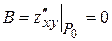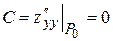
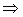
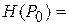
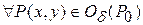
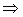
Следовательно, по теореме о достаточных условиях существования локального экстремума нельзя определенно ответить на вопрос о существовании экстремума в точке (0; 0). В данном случае стационарная точка (0; 0) является точкой локального минимума, поскольку, для (0; 0)=0.

Дата добавления: 2014-01-05