Метод планов скоростей и ускорений

Лекция 4

Наглядное представление о величинах и направлениях скоростей и ускорений отдельных точек механизма дают планы скоростей и ускорений.

Планом скоростей (ускорений) звена называется графическое построение, представляющее собой пучок, лучи которого изображают абсолютные скорости (ускорения) точек звена механизма, а отрезки, соединяющие концы лучей – относительные скорости (ускорения) соответствующих точек при заданном положении звена.

Планом скоростей (ускорений) механизма называется совокупность планов скоростей (ускорений) всех звеньев механизма, имеющих один общий полюс.

Построение планов скоростей и ускорений основано на графическом решении векторных уравнений распределения скоростей и ускорений.

Рассмотрим два характерных случая.

1. Две точки A и B (рис..10) принадлежат одному звену и расположены на расстоянии l_АB.

Рис. 10	Скорости точек A и B звена ABC	Рис. 11	План скоростей точек A и B звена ABC

Зависимость между скоростями точек A и B может быть представлена векторным уравнением , т.е. скорость точки B равна геометрической сумме скорости точки A в переносном поступательном движении и скорости точки B во вращательном относительном движении звена относительно точки A, при этом 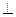АВ, т.к. траектория точки B в относительном движении вокруг точки A есть окружность с радиусом АВ.

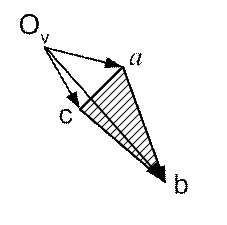
Изобразим скорости точек A и B в масштабе μ _v отрезками O_vа и O_vb, отложенными из одной точки O_v (рис. 11). Соединим концы отрезков (точки a и b) прямой линией. Полученный треугольник O_vab называется планом скоростей звена, а точка O_v – полюсом плана скоростей.

Для определения скоростей остальных точек звена, пример точки C, можно также воспользоваться векторными уравнениями. Однако в тех случаях, когда известны скорости двух точек звена, скорости остальных точек удобнее находить, используя теорему подобия для планов скоростей. Сформулируем эту теорему без доказательства: отрезки прямых линий, соединяющих точки на плане звена и отрезки прямых линий, соединяющих концы векторов скоростей, образуют подобные и сходственно расположенные фигуры. Признаком сходственного расположения служит порядок букв при обходе контура в определенном направлении. Так, при обходе треугольника abc в том же направлении порядок расположения букв одинаков. Таким образом, при использовании правила подобия в плане скоростей необходимо соблюдать при построении подобных фигур правило обхода контура.

Угловая скорость ω _АВ определяется по формуле

,

где V_BA – относительная скорость точки B во вращательном движении вокруг точки A.

Направление ω _АВ можно определить, если в точке B (рис..10) приложить вектор .

Направление относительных скоростей определяется из плана скоростей. При этом отрезок, определяющий относительную скорость, читается обратно обозначению этой скорости. Например, вектор на плане скоростей будет представлен, как «ab», вектор как «bc».

Ускорения точек A и B связаны между собой векторным уравнением

, т.е. ускорение точки B представляет собой геометрическую сумму ускорения 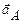точки A в переносном поступательном движении и ускорения 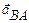точки B во вращательном относительном движении точки B вокруг точки A.

Полное относительное ускорение складывается в свою очередь из двух составляющих: нормального , направленного к центру относительного вращения, т.е. от точки B к точке A и касательного 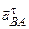, направленного перпендикулярно отрезку AB (рис. 12).

Рис. 12	Ускорения точек A и B звена ABC	Рис. 13	План ускорений звена ABC

Следовательно . Модуль нормального ускорения определяем по формуле

,

где ω _АВ – угловая скорость звена ABC, которая определяется из плана скоростей, как указано выше.

На рис.13 представлен план ускорений звена ABC. Ускорения точек A и B изображены на плане в масштабе μ _а отрезками π а' и π b', отложенными из общего полюса π.

Для определения ускорения точки C удобно использовать теорему подобия в плане ускорений: отрезки прямых линий, соединяющие точки на плане звена и отрезки прямых линий, соединяющих концы векторов полных ускорений этих точек на плане ускорений, образуют подобные и сходственно расположенные фигуры. При построении фигуры на плане необходимо соблюдать правило обхода контура, сформулированное выше.

Из плана ускорений можно определить величину и направление углового ускорения звена.

.

Направление углового ускорения определим, если в точке B (рис. 12) приложим вектор nb' ускорения .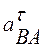

2. Две точки (А_x и А ₁) принадлежат двум звеньям – кулисе x-x и ползуну/1, и в данный момент времени совпадают (рис. 14). Кулиса и ползун образуют поступательную кинематическую пару.

Рис. 14	Скорости точек Ax направляющей и A 1 ползуна	Рис. 15	План скоростей точек Ax направляющей и A 1 ползуна

Скорость точки А ₁, принадлежащей ползуну 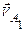будет складываться из двух скоростей – переносной 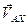, вместе с точкой А_x и относительной . Векторное уравнение имеет вид:

,

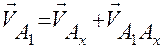где – скорость точки А_x, принадлежащей направляющей (кулисе) x-x, совпадающий в данный момент времени с точкой А ₁, принадлежащей ползуну (звено 1); 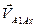– скорость ползуна относительно направляющей, направленная параллельно оси x-x.

План скоростей для этого случая представлен на рис. 15.

Ускорение точки А ₁ ползуна, когда переносное движение является вращательным, складывается из трех составляющих: переносного, т.е. ускорения точки А_x направляющей, Кориолисова (поворотного) точки ползуна А ₁ относительно направляющей А_x и относительного А ₁ относительно/ А_x.

.

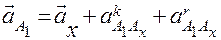Кориолисово ускорение вычисляется по формуле:

,

где ω _x – угловая скорость направляющей (кулисы) x-x. Направление Кориолисова ускорения определим, повернув вектор относительной скорости на 90° в направлении вращения направляющей, т.е. по направлению ω _x.

Вектор относительного ускорения ползуна относительно направляющей направлен параллельно оси x-x.

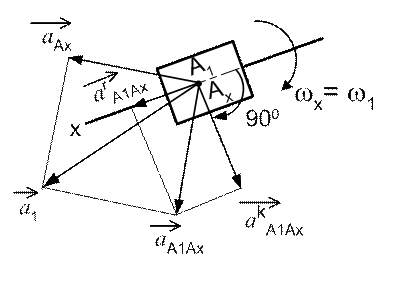
Вектора ускорений точек кулисы А_x и ползуна А ₁ показаны на рис..16, план ускорений для этого случая изображен на рис..17.

Рис. 16	Ускорения точек направляющей Ax и ползуна A 1	Рис. 17	План ускорений точек направляющей Ax и ползуна A 1

В частном случае, когда направляющая неподвижна, , , 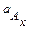и равны нулю и построение планов скоростей и ускорений значительно упрощается.

Дата добавления: 2014-01-05