План ускорений

Определим вначале ускорение точки A кривошипа, который вращается с постоянной угловой скоростью по окружности радиуса l_OA.

.

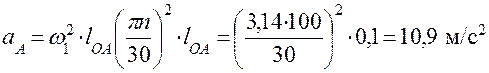Это нормальное ускорение точки A вокруг точки O изображаем отрезком π а', длину которого рекомендуется принимать в пределах 70...200/мм. В рассматриваемом примере π а' имеет длину 70 мм. Масштаб плана ускорений

.

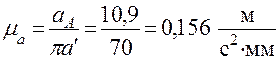Так как ω₁=const и e₁=0, то ускорение точки A состоит только из нормального и вектор π a' направлен перпендикулярно звену АО от точки A к центру вращения О.

В группе Асcура (2,3) определяем ускорение внутренней точки B. Рассматривая вначале движение точки B совместно с точкой A и относительно неё, а затем движение точки B относительно точки D запишем два векторных уравнения:

Ускорения точек A и D известны (а_D =0). Нормальные ускорения а_ВА и а_ВD определим по формулам:

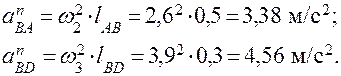
Вектор направлен параллельно звену АВ от точки B к точке A; вектор 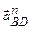– параллельно звену DB от точки B к точке D. У векторов касательных (тангенциальных) ускорений известны только направления; 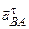/направлен перпендикулярно звену АВ, 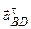– перпендикулярно BD. Определим длины отрезков a'n ₂ изображающего нормальное ускорение 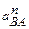и πn ₃ изображающего .

Решаем векторные уравнения графически. В соответствии с первым векторным уравнением из точки a' откладываем отрезок a'n ₂ и через точку n ₂ проводим линию, перпендикулярную шатуну AB. В соответствии со вторым уравнением из полюса π откладываем отрезок π n ₃ и через конец этого отрезка проводим линию перпендикулярно стороне BD коромысла BDC. На пересечении этих двух линий отмечаем точку b', соединив которую с полюсом получим вектор 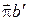, изображающий в масштабе полное ускорение точки В. Соединив точки a' и b' получаем вектор , изображающий полное относительное ускорение 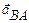точки В относительно точки А. Используя принцип подобия в плане ускорений на отрезке π b' строим треугольник 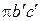подобный треугольнику DBC. Соединив полюс с точкой c', получаем вектор полного ускорения точки C. Используя этот же принцип определим ускорения центров тяжести звеньев 2 и 3. Для этого достаточно соединить полюс π с точками и 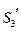расположенными соответственно в центрах тяжести отрезка a'b' и треугольника π b'c'.

В группе Ассура (3,4) известны ускорения точки c звена 3 и неподвижной точки Е_х, расположенной на направляющей х-х и совпадающей в данный момент с точкой Е, принадлежащей ползуну. Запишем два векторных уравнения для внутренней точки группы Ассура, рассматривая её движение совместно с точкой C и относительно неё, а затем совместно с точкой Е_х, принадлежащей направляющей и относительно этой точки:

.

В этих уравнениях вектор известен, ускорения a_Ex и a_EEx^k равны нулю, т.к. направляющая х-х неподвижна. Величину нормального ускорения a_ECⁿ точки Е относительно точки C определяем так же, как и в первой группе Ассура.

.

Вектор касательного ускорения точки Е относительно точки C направлен перпендикулярно звену СЕ, а относительное ускорение а_ЕЕх точки/ E в движении по направляющей направлено параллельно этой направляющей х-х. Решаем векторные уравнения графически. В соответствии с первым уравнением, из конца вектора откладываем отрезок c'n ₄, изображающий ускорение a_ECⁿ. Длина этого отрезка

.

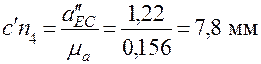Отрезок c'n ₄ проводим параллельно звену СЕ от точки E к точке C. Через точку n ₄ проводим линию, перпендикулярно звену СЕ.

В соответствии со вторым уравнением, учитывая, что два первых ускорения равны нулю, проводим через полюс π отрезок, параллельный направляющей х-х до пересечения с линией, проведенной перпендикулярно ВС из точки n ₄. Точка пересечения и есть искомая точка e', а вектор определяет ускорение ползуна 5. Положение точки S ₄ определяем по принципу подобия, поделив вектор полного относительного ускорения на две равные части. Проводим через полюс вектор ,определяющий ускорение центра тяжести шатуна СЕ. Из построенного плана ускорений определим ускорения точек.

Рис. 21 План ускорений механизма. μ _а = 0,156 м/с²·мм

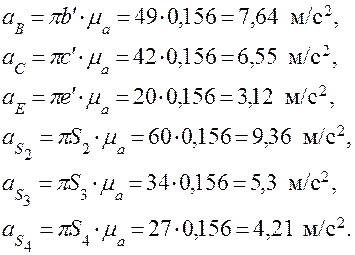
Величины угловых ускорений ε₂ ε₃ ε₄ звеньев 2,3 и 4 определим из уравнений:

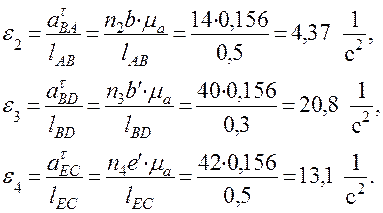
Перенесем вектор касательного ускорения 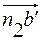точки B относительно точки A с плана ускорений в точку B плана механизма и пойдем направление углового ускорения ε₂ звена АВ. В данном случае ε₂ направлена против часовой стрелки. Аналогично походим направления ускорений ε₃ и ε₄. Поместим вектор 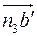, изображающий касательное ускорение 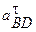в точку B плана механизма. Направление углового ускорения звена 3 так же, как и направление угловой скорости ω₃ совпадает с направлением движения часовой стрелки. И, наконец, переносим вектор 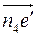, изображающий ускорение в точку Е и определяем, что угловое ускорение звена 4 направлено против часовой стрелки. Сравнивая направления угловых скоростей и угловых ускорений, делаем вывод, что звенья 3 и 4 вращаются ускоренно, а звено 2 – замедленно.

Дата добавления: 2014-01-05