
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы возможных направлений
|
|
|
|
Непосредственное решение задачи условной оптимизации, основанное на движении из одной допустимой точки, где выполнены все ограничения, к другой допустимой точке с лучшим значением целевой функции.
Методы связаны с нахождением предела 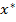 последовательности
последовательности 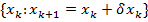 допустимых точек при
допустимых точек при  , таких, что
, таких, что 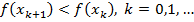 .
.
· Метод проекции градиента
1. Применение в задаче с ограничениями типа равенств
Построение последовательности точек, вычисляемых по правилу

где 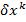 – вектор, вычисляемый для каждого значения k из условия проекции вектора
– вектор, вычисляемый для каждого значения k из условия проекции вектора 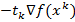 на аппроксимирующую плоскость, задаваемую уравнением
на аппроксимирующую плоскость, задаваемую уравнением  , которая аппроксимирует в точке
, которая аппроксимирует в точке 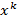 поверхность, задаваемую уравнениями
поверхность, задаваемую уравнениями  .
.

Вектор 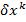 определяется по формуле
определяется по формуле 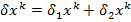 , где
, где 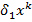 называется градиентной составляющей приращения, она равна
называется градиентной составляющей приращения, она равна

и обладает следующим свойством: градиентная составляющая приращения 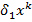 в линейном приближении не меняет вектор невязки условий связи, т.е. под действием градиентной составляющей точка
в линейном приближении не меняет вектор невязки условий связи, т.е. под действием градиентной составляющей точка 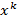 движется параллельно или по плоскости
движется параллельно или по плоскости  .
.
Составляющая 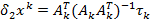 называется компенсационной составляющей приращения. Эта составляющая обладает, в линейном приближении, свойством компенсировать вектор невязки условий связи на величину
называется компенсационной составляющей приращения. Эта составляющая обладает, в линейном приближении, свойством компенсировать вектор невязки условий связи на величину  . Под действием составляющей
. Под действием составляющей  осуществляется проекция точки
осуществляется проекция точки 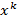 на плоскость
на плоскость  .
.
Величина шага 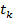 может выбираться как из условия убывания
может выбираться как из условия убывания 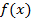 при переходе из точки
при переходе из точки 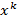 в точку
в точку 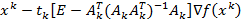 , так и из условия
, так и из условия
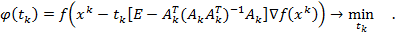
Расчет заканчивается в точке 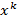 , в которой
, в которой  ,
, 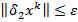 . В полученной точке
. В полученной точке 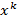 требуется обязательная проверка выполнения достаточных условий минимума задачи (УО). Точное равенство
требуется обязательная проверка выполнения достаточных условий минимума задачи (УО). Точное равенство  свидетельствует о точном выполнении необходимых условий экстремума, при этом вектор множителей Лагранжа определяется по формуле
свидетельствует о точном выполнении необходимых условий экстремума, при этом вектор множителей Лагранжа определяется по формуле

Знание приближения  вектора
вектора 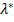 позволит осуществить проверку достаточных условий в точке
позволит осуществить проверку достаточных условий в точке 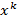 .
.
|
|
|
Обоснование. Проекцией точки 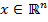 на множество
на множество 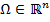 называют ближайшую к
называют ближайшую к 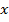 точку
точку  этого множества и обозначают ее
этого множества и обозначают ее 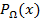 , т.е. такую точку
, т.е. такую точку 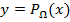 , что
, что

где 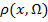 – расстояние от точки (элемента)
– расстояние от точки (элемента) 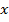 до множества
до множества 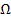 .
.
Основные свойства операции проектирования.
а) Если 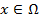 , то
, то 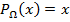 .
.
б) Если 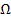 – замкнутое множество, то любая точка
– замкнутое множество, то любая точка 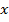 имеет проекцию
имеет проекцию 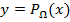 на множество
на множество 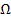 . Если при этом
. Если при этом 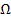 – выпуклое множество, то проекция единственна.
– выпуклое множество, то проекция единственна.
в) Точка 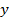 является проекцией точки
является проекцией точки 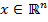 на замкнутое выпуклое множество
на замкнутое выпуклое множество 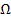 тогда и только тогда, когда для любой точки
тогда и только тогда, когда для любой точки 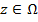 выполнено неравенство
выполнено неравенство
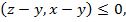
т.е. угол между векторами  не является острым.
не является острым.
г) Если 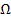 – выпуклое замкнутое множество,
– выпуклое замкнутое множество,  и
и 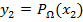 − проекции точек
− проекции точек 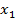 и
и 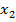 на
на 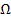 , то
, то

т.е. длина проекции отрезка на выпуклое множество не превосходит длины самого отрезка.
Результатом проектирования точки 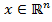 на замкнутое множество
на замкнутое множество 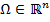 является точка
является точка  , либо совпадающая с
, либо совпадающая с 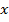 , если
, если 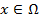 , либо лежащая на его границе
, либо лежащая на его границе 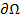 . Это свойство операции проектирования позволяет при численном решении задачи оптимизации с ограничениями на каждой k -й итерации использовать обычный метод градиентного спуска в направлении антиградиента из точки
. Это свойство операции проектирования позволяет при численном решении задачи оптимизации с ограничениями на каждой k -й итерации использовать обычный метод градиентного спуска в направлении антиградиента из точки 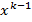 в точку
в точку 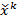 , а затем находить проекцию
, а затем находить проекцию 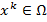 точки
точки 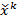 на множество
на множество 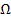 . Если при этом
. Если при этом 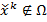 , то операция проектирования как бы возвращает ее обратно в допустимое множество
, то операция проектирования как бы возвращает ее обратно в допустимое множество 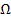 .
.
В случае ограничений типа равенств множество 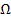 является выпуклым. Если целевая функция является строго выпуклой, то найденная точка гарантированно является точкой минимума.
является выпуклым. Если целевая функция является строго выпуклой, то найденная точка гарантированно является точкой минимума.
Утверждение (сходимость). Пусть 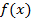 выпуклая, дифференцируемая на
выпуклая, дифференцируемая на 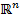 функция, градиент которой удовлетворяет на множестве
функция, градиент которой удовлетворяет на множестве  условию Липшица с константой L. Пусть множество
условию Липшица с константой L. Пусть множество 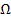 − выпуклое и замкнутое, множество решений задачи (УО) не пусто, а
− выпуклое и замкнутое, множество решений задачи (УО) не пусто, а 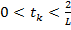 . Тогда
. Тогда 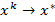 и, если
и, если 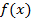 сильно выпукла, то
сильно выпукла, то 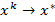 со скоростью геометрической прогрессии.
со скоростью геометрической прогрессии.
Определение: Функцию 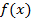 , определенную на выпуклом множестве
, определенную на выпуклом множестве 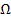 называют сильно выпуклой, если
называют сильно выпуклой, если  .
.
|
|
|
Всякая сильно выпуклая функция является строго выпуклой. Геометрически сильная выпуклость функции означает, что график функции 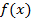 на плоскости расположен не только ниже секущей, соединяющей точки A и B, но и параболы, проходящей через эти точки, прогиб которой определяется параметром
на плоскости расположен не только ниже секущей, соединяющей точки A и B, но и параболы, проходящей через эти точки, прогиб которой определяется параметром  .
.
2. Применение в задаче с ограничениями типа неравенств

Стратегия поиска решения задачи учитывает тот факт, что решение 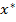 может лежать как внутри, так и на границе множества допустимых решений.
может лежать как внутри, так и на границе множества допустимых решений.
Для определения приближения решения 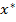 строится последовательность точек
строится последовательность точек 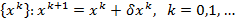 , где
, где 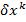 определяется в каждой точке
определяется в каждой точке 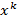 в зависимости от того, где ведется поиск – внутри или на границе множества допустимых решений.
в зависимости от того, где ведется поиск – внутри или на границе множества допустимых решений.
Решение задачи начинается с обхода границы допустимой области. Обход границ множества допустимых решений связан с выявлением активных в точке 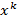 ограничений
ограничений 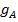 , аппроксимацией их плоскостью
, аппроксимацией их плоскостью

где  – матрица размера
– матрица размера 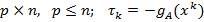 , и проекцией на нее вектора
, и проекцией на нее вектора 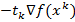 . Для выявления неравенств, активных в точке
. Для выявления неравенств, активных в точке 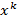 , задается погрешность определения активных ограничений
, задается погрешность определения активных ограничений  . Активными считаются те ограничения, для которых
. Активными считаются те ограничения, для которых 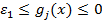 . Число p активных в точке
. Число p активных в точке 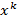 ограничений не должно превышать n.
ограничений не должно превышать n.
Поиск активных в точке ограничений рассматривается как самостоятельная задача, которая может быть решена путем последовательных приближений. Задается точка 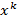 и вычисляется
и вычисляется 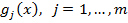 . Если
. Если 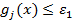 , то выбираются любые p ограничений с наименьшими по абсолютной величине невязками
, то выбираются любые p ограничений с наименьшими по абсолютной величине невязками 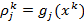 в точке
в точке 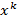 , строится матрица
, строится матрица 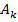 , вычисляется
, вычисляется  и находится точка
и находится точка
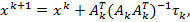
затем снова вычисляются невязки выбранных p ограничений. Уточнение по последней формуле осуществляется до тех пор, пока не будет найдена точка 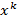 , в которой
, в которой 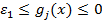 .
.
Проекция 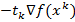 в точке
в точке 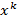 , в которой активны p ограничений, определяется точкой
, в которой активны p ограничений, определяется точкой

где приращение 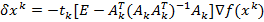 мосуществляет движение по плоскости
мосуществляет движение по плоскости  в направлении убывания
в направлении убывания 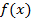 . Величина
. Величина 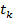 выбирается так:
выбирается так:  , где
, где 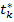 есть шаг, при котором
есть шаг, при котором
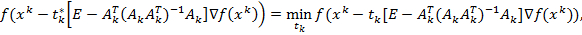
а 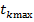 –наименьший шаг, при котором
–наименьший шаг, при котором
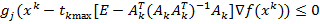
для всех ограничений, которые не были активными в точке 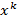 . Разумеется невязка ограничений в точке
. Разумеется невязка ограничений в точке 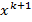 изменяется, поэтому вычислению точки
изменяется, поэтому вычислению точки  должна предшествовать процедура выбора активных ограничений, описанная выше.
должна предшествовать процедура выбора активных ограничений, описанная выше.
Процедура точек последовательности 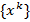 обеспечивает последовательное движение вдоль границы допустимой области. При выполнении неравенства
обеспечивает последовательное движение вдоль границы допустимой области. При выполнении неравенства  , вычисляется приближение
, вычисляется приближение 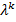 вектора множителей Лагранжа
вектора множителей Лагранжа 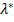 :
:
|
|
|
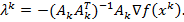
Если 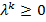 , то в точке
, то в точке 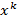 выполнены необходимые условия минимума и в ней должны быть проверены достаточные условия. Если среди множителей
выполнены необходимые условия минимума и в ней должны быть проверены достаточные условия. Если среди множителей 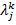 есть отрицательные, то
есть отрицательные, то 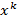 не является приближением
не является приближением 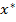 , так как в ней не выполнены необходимые условия минимума задачи (УО). Однако, выбор шага
, так как в ней не выполнены необходимые условия минимума задачи (УО). Однако, выбор шага 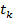 позволяет говорить о том, что значение
позволяет говорить о том, что значение 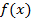 не может быть уменьшено при заданном составе активных ограничений и, следовательно, процесс минимизации
не может быть уменьшено при заданном составе активных ограничений и, следовательно, процесс минимизации 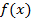 необходимо продолжить, уменьшив их число: в число пассивных переводится то из ограничений, которому соответствует наибольший по абсолютному значению отрицательный множитель
необходимо продолжить, уменьшив их число: в число пассивных переводится то из ограничений, которому соответствует наибольший по абсолютному значению отрицательный множитель 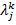 . Такая процедура поиска позволяет отыскать решение, лежащее как на границе, так и внутри множества допустимых решений.
. Такая процедура поиска позволяет отыскать решение, лежащее как на границе, так и внутри множества допустимых решений.
Утверждение о сходимости как для случая равенств.
· Метод возможных направлений Зойтендейка
Ненулевой вектор d называется возможным направлением в точке 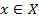 , если существует такое
, если существует такое 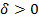 , что
, что 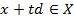 для всех
для всех 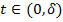 .
.
Вектор d называется возможным направлением спуска в точке 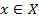 , если существует такое
, если существует такое 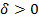 , что
, что  и
и 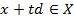 для всех
для всех 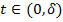 .
.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1590; Нарушение авторских прав?; Мы поможем в написании вашей работы!