Матричное представление трехмерных преобразований

Аналогично тому, как двумерные преобразования описываются матрицами размером 3x3, трехмерные преобразования могут быть представлены в виде матриц размером 4x4. И тогда трехмерная точка (x, у, z) записывается в однородных координатах как (W∙x, W∙y, W∙z, W), где W≠0. Если W≠1, для получения трехмерных декартовых координат точки (х, у, z) первые три однородные координаты делятся на W. Отсюда, в частности, следует, что две точки Η₁ и H₂ в пространстве однородных координат описывают одну и ту же точку трехмерного пространства в том и только в том случае, когда H₁=cH₂ для любой константы с, не равной нулю.

Трехмерная система координат, применяемая в этой книге, является правосторонней (рис.2.4). Примем соглашение, в соответствии с которым положительными будем считать такие повороты, при которых (если смотреть с конца положительной полуоси в направлении начала координат) поворот на 90° против часовой стрелки будет переводить одну положительную полуось в другую. На основе этого соглашения строится следующая таблица, которую можно использовать как для правых, так и для левых систем координат:

Рис. 2.4. Правосторонняя система координат

Таблица 2.2. Правосторонняя система координат

Если ось вращения	Положительным будет направление поворота
x у z	от у к z от z к x от x к y

Мы применяем здесь правостороннюю систему координат, поскольку она хорошо знакома большинству людей, хотя в трехмерной графике чаще более удобна левосторонняя система, так как ее легче представить наложенной на поверхность экрана дисплея. Это позволяет естественно интерпретировать тот факт, что точки с большими значениями z находятся дальше от наблюдателя. Отметим, что в левосторонней системе положительными будут повороты, выполняемые по часовой стрелке, если смотреть с конца положительной полуоси в направлении начала координат.

Трехмерный перенос является простым расширением двумерного:

Масштабирование расширяется аналогичным образом:

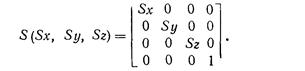
В самом деле,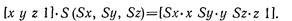

Двумерный поворот является в то же время трехмерным поворотом вокруг оси z. В трехмерном пространстве поворот вокруг оси z описывается выражением

Это легко проверить: в результате поворота на 90° вектора [1 0 0 1], являющегося единичным вектором оси х, должен получиться единичный вектор [0 1 0 1] оси y. Вычисляя произведение

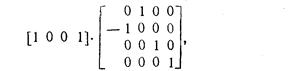
получаем предсказанный результат [0 1 0 1]. Матрица поворота вокруг оси x имеет вид

Матрица поворота вокруг оси у записывается в виде

Столбцы (и строки) верхней левой подматрицы размером 3x3 матриц Rz, Rx и Ry представляют собой взаимно ортогональные единичные векторы, интерпретация которых такая же, что и в двумерном случае.

Все эти матрицы преобразований имеют обратные матрицы. Матрица, обратная Т, получается подстановкой знака минус перед Dx, Dy и Dz; обратная S — заменой Sx, Sy и Sz на обратные им значения, а для каждой из трех матриц поворота — выбором отрицательного угла поворота.

Дата добавления: 2014-01-05