
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Независимость и полнота системы аксиом Вейля
|
|
|
|
Определение 3
Непротиворечивая система аксиом называется независимой, если каждая ее аксиома не зависит от всех остальных.
Независимость каждой аксиомы А в системе аксиом W проверяют доказательством непротиворечивости вспомогательной системы аксиом 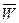 , которая составляется из данной заменой проверяемой аксиомы противоположным предложением. Для каждой аксиомы вспомогательная система составляется заново. Если проверка показывает, что все аксиомы независимы, то говорят, что система независима. Очевидно, что проверка требования независимости системы аксиом трудоемка. Требование независимости – желательное.
, которая составляется из данной заменой проверяемой аксиомы противоположным предложением. Для каждой аксиомы вспомогательная система составляется заново. Если проверка показывает, что все аксиомы независимы, то говорят, что система независима. Очевидно, что проверка требования независимости системы аксиом трудоемка. Требование независимости – желательное.
Определение 4
Непротиворечивая система аксиом называется полной, если все ее модели изоморфны, т.е. существует биективное (взаимнооднозначное) отображение одной модели на другую, при котором точкам и векторам одной модели соответствуют точки и векторы другой модели и сохраняются все отношения, вводимые аксиомами.
Полная система аксиом не может быть дополнена никакими новыми аксиомами о ранее введенных отношениях, не зависящих от ранее введенных аксиом и не противоречащих им. Проверка полноты системы аксиом W сводится к проверке непротиворечивости еще одной вспомогательной системы W ¢, которая составляется из данной добавлением новой аксиомы А: 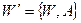 . Допустим, что непротиворечивая система аксиом W дополнена еще одной, не зависящей от W аксиомой А. Тогда аксиома А не может внести противоречие и
. Допустим, что непротиворечивая система аксиом W дополнена еще одной, не зависящей от W аксиомой А. Тогда аксиома А не может внести противоречие и 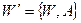 непротиворечива. Отрицание сводится к проверке непротиворечивости еще одной вспомогательной системы W ¢, которая составляется из данной добавлением новой аксиомы А:
непротиворечива. Отрицание сводится к проверке непротиворечивости еще одной вспомогательной системы W ¢, которая составляется из данной добавлением новой аксиомы А: 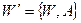 .
.
Примером неполной системы аксиом является система аксиом абсолютной геометрии, состоящая из аксиом четырех групп аксиоматики Гильберта: связи (инцидентности или принадлежности), порядка, движения, непрерывности. Она может быть дополнена аксиомой параллельности или ее отрицанием. Получат две непротиворечивые теории – геометрии Евклида и Лобачевского. Аксиоматики становятся полными и дальнейшее пополнение невозможно.
|
|
|
Докажем, что система W аксиом Вейля полна, т.е. все ее модели изоморфны. Для этого достаточно доказать, что любая модель W изоморфна арифметической модели, построенной выше.
Пусть М 0 – арифметическая модель, «точки» и «векторы» которой представляют упорядоченные тройки действительных чисел, а М – произвольная модель. Введем на М прямоугольную систему координат 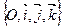 , что возможно на основании соответствующей теоремы. Тогда эта теорема будет реализована в любой модели.
, что возможно на основании соответствующей теоремы. Тогда эта теорема будет реализована в любой модели.
Установим отображение: «точке» А 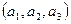 , А Î М, поставим в соответствие «точку»
, А Î М, поставим в соответствие «точку» 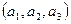 арифметической модели М 0; «вектору»
арифметической модели М 0; «вектору» 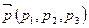 ,
, 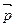 Î М – «вектор»
Î М – «вектор» 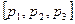 Î М 0. Получим биективное отображение
Î М 0. Получим биективное отображение 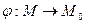 (объясните, почему?). Убедимся в том, что j сохраняет отношения.
(объясните, почему?). Убедимся в том, что j сохраняет отношения.
1) Если  ,
,  , то
, то  ;
;

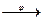
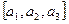 ,
, 
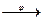
 ,
,
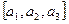 +
+ =
=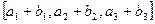 , т.е.
, т.е. 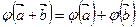 .
.
Отсюда следует, что сложение векторов сохраняется.
2) Если  и
и  , то
, то  ;
;

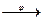
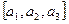 ,
, 
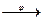
 = a
= a 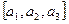 ,
,
т.е. 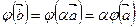 .
.
Следовательно, умножение вектора на действительное число сохраняется.
3) Если  ,
,  , то
, то 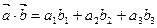 ;
;

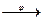
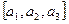 ,
, 
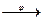
 ,
, 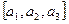 ×
× =
= , т.е.
, т.е. 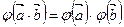
Отсюда следует, что скалярное умножение векторов сохраняется.
4) Если А 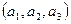 , В
, В 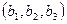 , то
, то 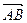
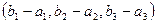 ;
;
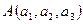
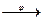
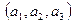 ,
, 
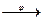
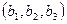 ,
,
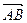
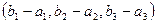
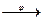
 .
.
Отношение связи точек и векторов сохраняется при отображении j.
Вывод: отображение j является изоморфизмом произвольной модели М и арифметической модели М 0. Исходя из транзитивности отношения изоморфизма, любые две модели изоморфны (докажите самостоятельно). Значит, система аксиом Вейля трехмерного евклидова пространства полная, а теория может быть построена на любой из них.
Если все модели некоторой системы аксиом изоморфны, то ее также называют категоричной.
|
|
|
Таким образом, система аксиом Вейля непротиворечива, независима и полна (категорична).
Построение евклидовой геометрии
на основе системы аксиом Вейля
Построение евклидовой геометрии состоит в том, что вводятся определения различных фигур (прямые, плоскости, отрезки, углы, треугольники и т.д.) и с помощью введенных аксиом Вейля доказываются их свойства.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 3174; Нарушение авторских прав?; Мы поможем в написании вашей работы!