Представление непериодических функций времени в частотной области. Интеграл Фурье

Ряд Фурье допускает представление в частотной области толь­ко периодических функций времени. Однако часто имеют дело с непериодическими функциями, характерными, например, для коммутационных процессов, молнии или разрядов статического электричества и т. д.

Мы исходим из комплексного ряда Фурье для периодических функций (пределы интегрирования –Т /2 и + Т /2):

(2.14)

Так как в линейчатом спектре ряда Фурье расстояние между спектральными линиями соответствует

можно также записать

(2.15)

Согласно определению интеграла по Риману

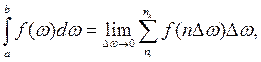(2.16)

при T → ∞, т. е. при Δ f → ∞ конечное расстояние между спект­ральными линиями Δ ω за знаком суммы переходит в бесконечно малое расстояние dω, дискретная переменная n Δ ω – в непре­рывную переменную ω, а сумма – в интеграл. Таким образом, получают интеграл Фурье для непериодической функции u (t) _непер:

(2.17)

где

(2.18)

преобразование Фурье, спектральная функция или спектраль­ная плотность u (t);

| Х (ω)| - плотность распределения амплитуд.

Для непериодической функции u (t) преобразование Фурье имеет вид

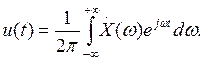(2.19)

Следовательно, преобразование Фурье и его обращение взаимообратны с точностью до множителя 1/2π.

Название "спектральная плотность" происходит от того, что спектральная функция 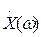идентична линейчатому спектру С_n отнесенному к расстоянию между соседними частотами. Так как , получаем

(2.20)

Если отнести амплитуды С_n к Δ f и образовать предельное значение для

Т → ∞ (соответственно Δ f → 0), получим

иначе говоря, спектральную плотность.

Если, например, линейчатый спектр измеряется в вольтах, то спектральная плотность сравнимого однократного про­цесса имеет размерность В/Гц.

Очевидно, непериодические процессы тоже могут быть пред­ставлены как наложение синусоидальных или косинусоидальных колебаний. Однако в отличие от периодических процессов здесь участвуют все частоты от - ∞ до + ∞ с амплитудами 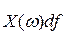. Так как при однократных процессах содержащаяся в одном импульсе конечная энергия распределяется на бесконечное множество ча­стот, то амплитуда отдельной спектральной составляющей долж­на быть бесконечно малой. Чтобы избежать этой неопределенно­сти, относят энергию импульса к частоте и получают таким обра­зом спектральную плотность, предельное значение которой при Δ f → 0 остается конечным и как раз соответствует преобразова­нию Фурье. Преобразование Фурье абсолютно монохроматичес­кого синусоидального колебания обладает бесконечно большой плотностью распределения амплитуд гармоник, потому что энер­гия сигнала распределяется на единственную частоту с шириной линии Δ f = 0 (импульсы Дирака). Аналитически это выражается в том, что интеграл Фурье от функции синуса не сходится, что подтверждает соответствие анализа физическим процессам. Вы­шеприведенные зависимости объясняют то, что показание изме­рителя напряжения помех или частичных разрядов зависит от его полосы пропускания Δ f. Чем больше полоса пропускания, тем больше измеряемое значение.

Если нанести на графике вплотную к линейчатому спектру периодической функции модуль спектральной плотности, полу­чим непрерывный спектр плотности распределения амплитуд непериодического процесса. Из преобразования Фурье для пря­моугольного импульса длительностью τ и амплитудой U_m

(2.21)

можно получить, например, "физическую" плотность распреде­ления амплитуд (2|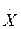| — измеренное значение) как

(2.22)

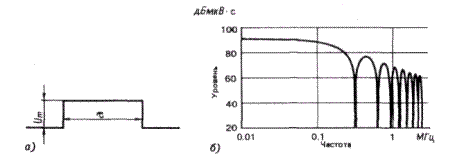
Рисунок 2.6 – Однократный прямоугольный импульс (а) и соответствующая "физи­ческая" плотность распределения амплитуд (б)

Прямоугольный импульс и соответствующая "физическая" плотность распределения амплитуд показаны на рисунке 2.6. Оче­видно, и непрерывный спектр одиночного прямоугольного им­пульса представляет функцию si (x) (sin х / х). Нулевые значения этой функции опять равнозначны величине обратной длитель­ности импульса. При низких частотах функция синуса совпадает со своим аргументом, так что начальное значение спектра про­порционально двойной площади импульса 2 U_mt. Для оси частот часто выбирают логарифмический масштаб, вследствие чего ну­левые значения функции si (x) не распределяются на одинаковых расстояниях, а с растущей частотой плотнее располагается друг к другу.

3 ПАССИВНЫЕ ПОМЕХОПОДАВЛЯЮЩИЕ КОМПОНЕНТЫ

Дата добавления: 2014-01-05