Геометрическая оптика

Устройство большого числа оптических приборов базируется на представлении о световых лучах, распространяющихся прямолинейно в однородном веществе и испытывающих отражения и преломления на границах раздела. Отдел оптики, который рассматривает теорию таких приборов, носит название лучевой, или геометрической, оптика. Лучевая оптика использует два закона: закон отражения и закон преломления. Как мы увидим дальше, для выяснения всех свойств оптических приборов недостаточно этих двух законов. Во-первых, должны быть учтены фотометрические соотношения, для выяснения яркости и освещенности изображения. Во-вторых необходимо учесть роль явлений интерференции и диффракции света, дающих границу применимости представлении о прямолинейном распространении света. Однако, несмотря ил большую важность этих явлений, первоначальная теория оптических приборов может базироваться лишь на законах лучевой оптики.

В основу геометрической оптики вместо перечисленных выше законов может быть положен так называемый принцип Ферма. Согласно этому принципу, свет распространяется по такому пути, для прохождения которого ему требуется минимальное время, Точнее, это время должно быть экстремальным, т. е. либо минимальным, либо максимальным, либо стационарным — одинаковым для всех возможных путей. В последнем случае все пути света между двумя точками оказываются таутохронными (требующими для своего прохождения одинакового времени).

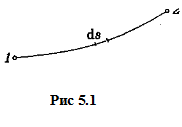
Участок пути ds (рис. 5.1) свет проходит за время dt = ds/υ, где υ — скорость света в данном месте. Так как υ = с/n, то dt =n ds/с, и время τ для прохождения светом пути 1 —> 2 равно

где L называют оптической длиной пути. В однородной среде L=ns.

Из принципа Ферма действительно следуют все законы геометрической оптики.

Предположим теперь, что две среды с показателями преломления п ₁ и n ₂ разделяются сферической поверхностью Σ (рис. 5.2). На линии LL ', проходящей через центр нашей сферы О, поместим точечный источник света L. Рассмотрим узкий гомоцентрический конус лучей, падающий из L на поверхность раздела двух сред.

Мы предполагаем пучок настолько узким, т. е. угол ψ настолько малым, что практически можно считать отрезок LS равным LA, L ' S равным L'А и т. д. Такой узкий пучок будем называть параксиальным. Итак, условие параксиальности пучка есть

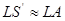и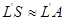

Возьмем какой-либо луч из этого пучка, например LA, падающий на Σ под утлом i, построим сопряженный ему преломленный луч AL ' (угол преломления r) и найдем положение точки, в которой преломленный луч пересечет ось системы.

Из треугольника ALO имеем

из треугольника OAL '

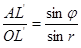
Отсюда

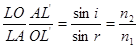
В дальнейшем все отрезки вдоль оси будем отсчитывать от точки S, считая положительными отрезки, откладываемые от S вправо (в направлении распространяющегося света), и отрицательными — отрезки, откладываемые влево. Таким образом,

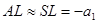, AO=SO=R

(радиус нашей сферы). В таком случае LO=-a ₁ +R, OL^’=a ₂ - R. Из формулы (4.3) получим

т. е.

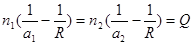
Последняя формула показывает, что произведение 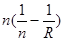при преломлении сохраняет свою величину Q. Его называют нулевым инвариантом Аббе. Для многих целей этой формуле удобно придать вид

(5.1)

Соотношение (5.1) позволяет найти длину a ₂= SL^’, если задано a₁=LS, т. е. позволяет отыскать положение точки L ' по заданному L. При выводе его мы, кроме закона преломления, пользовались еще допущением, что луч LA принадлежит к параксиальному пучку. Следовательно, соотношение справедливо для любого луча параксиального пучка. Из формулы (5.1) видно, что a₂ при заданных параметрах задачи (n₁, n₂, R) зависит только от a₁. Таким образом, все лучи параксиального гомоцентрического пучка, выходящего из L, пересекают ось в одной и тон же точке L ', которая является, следовательно, изображением источника L. Итак, гомоцентрический пучок при преломлении на сферической поверхности остается гомоцентрическим, если он удовлетворяет условию параксиальности. Основное уравнение (5.1) охватывает все случаи преломления лучей на сферической поверхности. Пользуясь установленным выше правилом знаков, мы можем разобрать случай выпуклой (R > 0) или вогнутой (R < 0) поверхности.

Точно так же в зависимости от того, будут ли a₁ и a₂ иметь разные знаки или одинаковые, мы будем иметь случаи, когда изображение располагается с противоположной по сравнению с источником стороны преломляющей поверхности или лежит по одну сторону с ним. В первом случае (a₂>0) точка, именуемая изображением, есть действительно точка пересечения преломленных лучей. Такое изображение называется действительным. Во втором случае (a₂ < 0), очевидно, преломленные лучи, идущие во второй среде, остаются расходящимися и реально не пересекаются. В этом случае название изображения относится к той воображаемой точке, которая представляет собой место пересечения предполагаемого продолжения преломленных лучей. Такое изображение называется мнимым. Наши рассуждения и формула (5.1) показывают, что гомоцентрический пучок после преломления направлен так, что его лучи или пересекаются в одной точке (действительное изображение), или могут быть представлены как пересекающиеся в одной точке (мнимое изображение). Именно в этом смысле он и остается гомоцентрическим. Так как для всех наших рассуждений нам важно знать направление световых лучей, то при всех построениях мы одинаково можем пользоваться как действительным, так и мнимым изображением.

Формула (5.1) показывает также, что если бы источник был в L^’, то изображение расположилось бы в L (взаимность).

Из основного уравнения (5.1) следует, что при a₁= -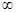

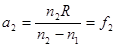(5.2)

при a₂=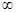

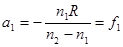(5.3)

т.е. f₁, f₂ зависят только от радиуса кривизны поверхности R и показателей преломления n₁, n₂ обеих сред.

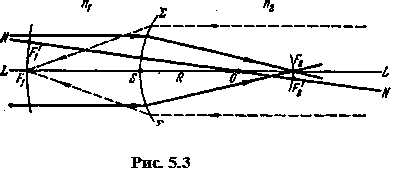
Величины f₁, f₂ суть постоянные длины, характеризующие преломляющую поверхность. Они называются ее фокусными расстояниями: f₁ — переднее фокусное расстояние (точка F₁ — передний фокус); f₂ — заднее фокусное расстояние (точка F₂ — задний фокус) (рис. 5.3).

Таким образом, фокусом сферической поверхности называется точка, в которой сходятся после преломления параллельные лучи (т. е. лучи, идущие из бесконечно удаленной точки). Понятно, что фокусы, так же как и изображения, могут быть действительными и мнимыми, т.е. представлять точку пересечения преломленных лучей (бывших до преломления параллельными) или их предполагаемых продолжений. Так, если вогнутая сторона поверхности раздела обращена к среде, имеющей меньший показатель преломления, то оба фокуса будут мнимыми. В этом легко убедиться самостоятельно.

Параллельные лучи, идущие справа налево вдоль- NO (см. рис. 5.3), сойдутся в фокусе F₁', расположенном на линии NO и лежащем также на расстоянии | f ₁| от преломляющей поверхности. Геометрическое место точек F ₁, F ₁’... образует сферическую поверхность с радиусом | R – f ₁| (для случая, показанного на рис. 5.3 f ₁ < 0), концентрическую с преломляющей сферой (с центром в точке O). Эта поверхность носит название передней фокальной поверхности.

Аналогично построим заднюю фокальную поверхность радиуса | f ₂ – R |. Малые участки этих поверхностей (для параксиальной области) могут быть приняты за плоскости (фокальные плоскости). Фокусные расстояния сферической поверхности различны по знаку и не равны между собой по абсолютной величине (см. рис. 5.3), ибо n ₁ # n ₂. Рассматриваемый случай легко осуществить па опыте, взяв широкую стеклянную трубку и заклеив один ее конец часовым стеклом, имеющим сферическую форму. Если налить в трубку воду или, еще лучше, бензол, показатель преломления которого практически совпадает с показателем преломления часового стекла, то получим сферическую границу раздела между воздухом (n ₁ = 1,00) и бензолом (n ₂ = 1,49).

Согласно сказанному в § 4, формулу (5.1) можно применить и к случаю отражения, если

положить п ₂ = - n ₁. Тогда имеем

1/ а ₁+1/ а ₂ = 2/ R

это формула сферического зеркала. Фокусное расстояние такого зеркала определится по формуле (5.2). Найдем f = R /2, и, следовательно, формуле зеркала можно придать вид:

1/ а ₁+1/ а ₂ = 1/ f

В случае зеркала изображение действительное, если оно лежит по одну сторону с источником, и мнимое, если расположено за зеркалом.

Случаи вогнутого и выпуклого зеркала отличаются лишь знаком R. Легко видеть, что фокус вогнутого зеркала – действительный, а фокус выпуклого зеркала — мнимый.

Чтобы получить законы плоского зеркала, достаточно положить R =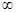. В этом случае найдем а ₁ = — а ₂, т.е. изображение точки в плоском зеркале мнимое и симметрично расположенное.

Дата добавления: 2014-01-05