Индуктивность контура. Индуктивность соленоида

Контур с током 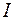создает через площадь, ограниченную им, магнитный поток , который зависит от индукции В (рис. 74.1). Так как В ~ I, то, следовательно, Ф~ I. Переходя к равенству, получаем:

, (74.1)

где L – коэффициент пропорциональности. Он характеризует магнитные свойства цепи, зависит от формы, размеров контура и среды, в которой находится, и называется индуктивностью контура. В этом отношении индуктивность контура оказывается похожей на электрическую емкость уединенного проводника, которая также зависит только от размеров, формы проводника и от диэлектрической проницаемости среды.

Из равенства (74.1) для индуктивности L получаем:

. (74.2)

Из формулы (74.2) следует, что индуктивность контура численно равна потоку, созданному током контура через площадь, им ограниченную, при силе тока в контуре, равной единице. Единица индуктивности в единицах СИ – генри (Гн). Из выражения (74.2) видно, что . Заметим, что индуктивностью называют также идеализированный элемент электрической цепи, в котором накапливается энергия магнитного поля.

Вычислим индуктивность соленоида, содержащего N витков и сердечник с магнитной проницаемостью 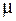(рис. 74.1). Индуктивность соленоида определим как коэффициент пропорциональности между полным магнитным потоком , созданным в нем, и силой тока :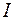

. (74.3)

Полный поток называется потокосцеплением.

Так как вектор 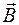перпендикулярен поперечному сечению соленоида, то поток, связанный с одним витком, равен , тогда полный поток (потокосцепление) для соленоида

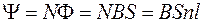, (74.4)

где n – число витков на единицу длины (плотность намотки).

Для поля соленоида согласно выражению (72.8) 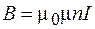. Подставив это выражение в формулу (74.4), получим:

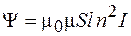. (74.5)

Сравнивая формулы (74.3) и (74.5), получаем для индуктивности соленоида:

. (74.6)

Так как 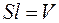– объем соленоида, то формулу (74.6) запишем в виде

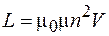. (74.7)

Отсюда следует, что индуктивность соленоида зависит от его размеров, плотности намотки и среды.

Из формулы (74.7) видно, что единицей магнитной постоян-ной 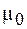является генри на метр (Гн/м), но из нее не следует явной зависимости индуктивности соленоида от силы тока в нем. Однако, если сердечник соленоида – ферромагнетик, то для него 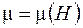, а так как для соленоида 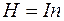, то, следовательно, . Но тогда и индуктивность соленоида становится функцией тока в нем: . Это следует учитывать при расчете индуктивности катушки, содержащей ферромагнитный сердечник.

Дата добавления: 2014-01-05