Контур с током в однородном магнитном поле

Рассмотрим случаи разного расположения контура в магнитном поле. Положение контура определяется углом между направлениями положительной нормали к контуру и магнитного поля. Направление положительной нормали связано с направлением тока в контуре правилом правого винта.

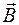1. Пусть , т. е. линии вектора лежат в плоскости контура (рис. 81.1). Для простоты будем рассматривать контур прямоугольной формы. Пусть а и b – размеры сторон контура. Воспользуемся законом Ампера (66.6). На сторону 1–2 дей-ствует сила

. (81.1)

На стороны 2–3 и 4–1 силы не действуют, так как эти стороны расположены параллельно линиям вектора 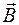. На сторону 3–4 действует сила

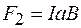. (81.2)

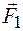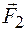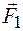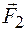Из формул (81.1) и (81.2) видно, что силы и равны по модулю . Кроме того, они параллельны, противоположно направлены и не действуют по одной прямой. Поэтому силы и образуют пару сил с плечом b. Они создают вращающий момент . После подстановки получаем:

,

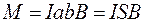где S – площадь контура.

Так как 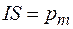(магнитный момент контура), то вращающий момент, действующий на контур, равен

. (81.3)

Этот вращающий момент стремится повернуть контур так, чтобы его магнитный момент 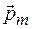установился по направлению вектора индукции 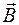магнитного поля.

2. Пусть теперь , т. е. вектор 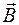перпендикулярен плоскости контура (рис. 81.2). Магнитное поле действует на каждую из сторон контура. Все четыре силы 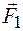, , 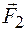, 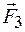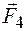лежат в одной плоскости. Так как поле однородно, то силы попарно уравновешивают друг друга и не могут вызвать перемещение контура. Действие этих сил сводится к тому, что они вызывают растяжение контура, деформируют его. Если изменить направление тока в контуре или направление магнитного поля, то контур будет сжиматься.

Таким образом, рассмотрев пункты 1 и 2, можно сделать вывод: магнитное поле, направленное вдоль плоскости рамки, создает вращающий момент; поле, направленное перпендикулярно, приводит к деформации.

3. Направления векторов и 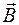образуют острый угол (рис. 81.3).

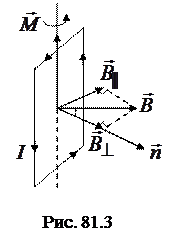Вектор магнитной индукции 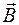разложим на две составляющие: 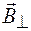– перпендикулярную к плоскости контура и – параллельную плоскости контура. Магнитное поле с индукцией 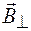вызывает деформацию контура. Магнитное поле с индукцией создает вращающий момент, который можно определить по формуле (81.3).

Поскольку 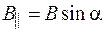, то вращающий момент равен

, (81.4)

где .

Выражение (81.4) определяет модуль векторного произведения векторов 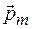и 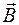, т. е. можно записать

(81.5)

По формуле (81.5) можно рассчитать вращающий момент сил, действующих на контур любой формы при любом его положении в однородном магнитном поле. Вращение контура с током в магнитном поле лежит в основе действия электроизмерительных приборов, электрических двигателей.

Однородное магнитное поле стремится повернуть контур так, чтобы угол между векторам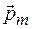и и 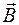уменьшился до нуля. Для увеличения угла на 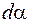нужно совершить против сил, действующих на него со стороны магнитного поля, работу 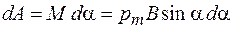. Эта работа идет на увеличение энергии взаимодействия контура с магнитным полем, 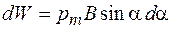. Выполнив интегрирование по переменной a, получим 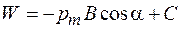. Постоянную интегрирования примем равной нулю. Тогда

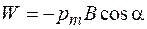(81.6)

или

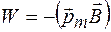. (81.7)

Следует отметить, что полученная формула аналогична выражению (44.5) для энергии диполя в электрическом поле.

Дата добавления: 2014-01-05