Модель гармонического осциллятора

Рассмотрим некоторые наиболее простые колебательные системы, которые позволяют понять ряд общих свойств таких систем.

а) Пружинный маятник

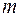Пусть груз массой движется без трения по горизонтальной плоскости под действием невесомой пружины с жесткостью 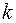, длина которой в нерастянутом состоянии 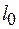(рис. 2.1).

При отклонении груза от положения равновесия на величину 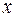на него будет действовать со стороны пружины упругая сила и по второму закону Ньютона можно записать

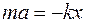. (2.1)

Разделив обе части уравнения на массу груза 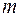, получим

.

Обозначим 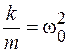, и тогда уравнение примет вид

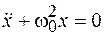. (2.2)

б) Физический маятник

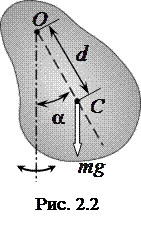
Физическим маятником называется твердое тело массой 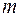, способное совершать колебания вокруг неподвижной точки, не совпадающей с центром масс этого тела (рис. 2.2).

В соответствии с основным уравнением динамики вращательного движения имеем

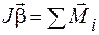, (2.3)

где 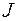– момент инерции маятника относительно оси вращение О; 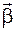– угловое ускорение; 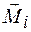– момент силы, действующей на маятник.

На маятник действуют две силы: сила тяжести и сила реакции опоры. Момент силы реакции опоры относительно оси вращения равен нулю, так как плечо этой силы равно нулю, поэтому в правой части равенства (2.3) остается только момент силы тяжести:

,

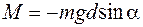где 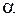– угол отклонения нити от положения равновесия; 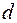– расстояние от оси вращения до центра масс С. Так как 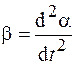, то уравнение (2.3) примет вид

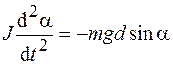. (2.4)

Если угол отклонения мал (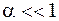), то и, деля обе части последнего уравнения на 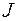, после преобразований получим

,

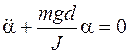где для сокращения записи введено обозначение .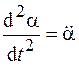

Обозначим 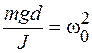, тогда уравнение примет окончательный вид

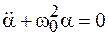. (2.5)

в) Математический маятник

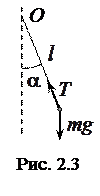Математическим маятником называется материальная точка массой 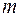, подвешенная на нерастяжимой невесомой нити длиной 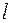и способная совершать колебания в поле сил тяжести (рис. 2.3).

Для материальной точки момент инерции равен 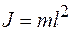. Подставляя это выражение в формулу (2.4), с учетом того, что 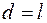, для малых углов отклонения 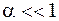вновь получим уравнение (2.5):

,

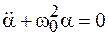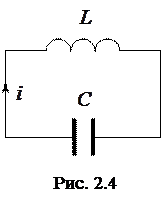где обозначено .

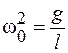г) LC-контур

Пусть в начальный момент времени 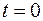конденсатору сообщен заряд 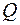, а затем к нему подключена катушка индуктивности 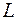, как показано на рисунке 2.4. Конденсатор начнет разряжаться через катушку индуктивности, и в цепи потечет ток. Одновременно в катушке в соответствии с законом электромагнитной индукции Фарадея возникнет ЭДС самоиндукции, величина которой будет равна 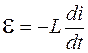. В результате действия ЭДС самоиндукции конденсатор перезарядится, т. е. заряд на обкладках конденсатора поменяет знак. После перезарядки конденсатор снова начнет разряжаться через катушку индуктивности, и этот процесс будет периодически повторяться во времени, т. е. в цепи возникнут электрические колебания.

По второму закону Кирхгофа ЭДС самоиндукции будет равна падению напряжения на конденсаторе 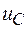, т. е.

.

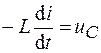Сила тока 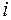равна первой производной по времени от величины заряда на обкладках конденсатора 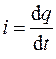, а напряжение на конденсаторе связано с зарядом 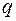соотношением 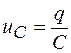. С учетом этого последнее уравнение можно записать в виде

.

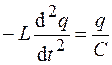Разделив обе части уравнения на 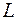и обозначив 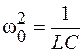, преобразуем полученное уравнение к виду

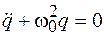, (2.6)

где по-прежнему вторая производная по времени обозначена двумя точками.

Дата добавления: 2014-01-05