Колебаний. Характеристики затухающих колебаний

Решение дифференциального уравнения затухающих

Строгий математический анализ уравнения (9.3) показывает, что его решение имеет вид гармонических колебаний при условии, когда потери энергии, характеризуемые коэффициентом затухания 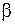, не превышают критического значения , равного частоте собственных колебаний 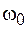, т. е.

. (10.1)

При выполнении этого условия общее решение дифференциального уравнения (9.3) можно записать следующим образом:

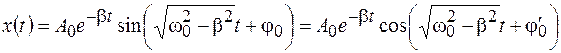, (10.2)

где . Из (10.2) можно сделать следующие выводы:

1) при наличии в колебательной системе потерь в ней будут происходить гармонические колебания, амплитуда которых уменьшается по экспоненциальному закону:

, (10.3)

2) частота затухающих колебаний 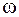меньше частоты 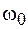собственных колебаний при отсутствии трения:

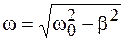. (10.4)

Так же, как и в случае незатухающих колебаний, начальные амплитуда 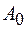и фаза 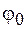определяются начальными условиями. График затухающих колебаний изображен на рисунке 10.1.

Из (10.4) следует, что период затухающих колебаний

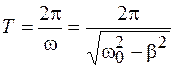. (10.5)

Величина, обратная коэффициенту затухания 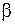, называется временем релаксации :

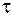. (10.6)

Если в выражение (10.3) подставить момент времени , то амплитуда затухающих колебаний будет равна . Отсюда становится ясным физический смысл времени релаксации: время релаксации – это время, в течение которого амплитуда затухающих колебаний уменьшается ве раз.

Натуральный логарифм отношения амплитуды колебаний в произвольный момент времени к амплитуде колебаний в момент времени 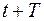, т. е. спустя период колебаний 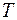, называется логарифмическим декрементом затухания :

. (10.7)

Из определения следует, что логарифмический декремент затухания есть величина безразмерная. Подставляя в (10.7) амплитуды колебаний из (10.3), получим

. (10.8)

Так как , то величина характеризует число колебаний , происходящих за время релаксации 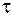. Поэтому декремент затухания есть величина, обратная числу колебаний, происходящих за время, в течение которого амплитуда уменьшается в е раз:

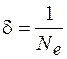. (10.9)

Для характеристики потерь в колебательной системе вводится еще одна важная характеристика, называемая добротностью. Добротностью 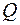колебательной системы называется отношение полной энергии колебаний в произвольный момент времени к потерям энергии за последующий период, умноженное на :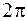

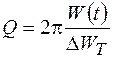, (10.10)

где .

Из формулы (10.10) следует, что добротность также является безразмерной величиной. В случае малых потерь добротность связана с декрементом затухания соотношением

. (10.11)

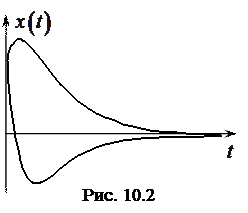
Как видно из выражений (10.4), (10.5), при увеличении потерь частота затухающих колебаний уменьшается, а их период соответственно увеличивается. При достижении критических потерь 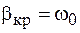частота равна нулю, а период – бесконечности. Это означает, что колебания в системе отсутствуют, процесс становится апериодическим и имеет, в зависимости от начальных условий, один из изображенных на рисунке 10.2 видов.

Дата добавления: 2014-01-05