Дифракция на круглом отверстии и диске

Графическое сложение амплитуд.

Качественный, а в простейших случаях и количественный анализ дифракционной картины можно проделать с помощью метода графического сложения амплитуд. Для этого плоскость препятствия, на котором дифрагирует волна, разбивается на малые участки. Амплитуда волны, приходящей от каждого участка, изображается вектором соответствующей длины. Так как разность хода от разных участков до точки наблюдения оказывается различной, то векторы повернуты относительно друг друга на угол, равный разности фаз приходящих волн. В соответствии с принципом суперпозиции амплитуда результирующей волны равна векторной сумме амплитуд волн от всех участков.

Применим метод сложения амплитуд для анализа дифракции плоской волны на круглом отверстии. Дифракционная картина имеет вид концентрических темных и светлых колец, как показано на рисунке 56.1. Для определения интенсивности излучения в центре картины разобьем отверстие на малые кольцевые зоны равной площади 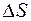(меньшие, чем зоны Френеля). От каждого такого кольца в точку наблюдения будет приходить элементарная волна амплитудой 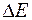. Эти волны, имеющие примерно равные амплитуды, но отличающиеся по фазе в соответствии с изменением оптической длины пути от кольцевой зоны до точки наблюдения, будут складываться в этой точке. На векторной диаграмме они изобразятся стрелками одинаковой длины, но повернутыми относительно друг друга на некоторый угол 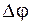. Если радиус отверстия больше радиуса первой зоны Френеля (случай дифракции Френеля), то векторная диаграмма будет иметь вид, изображенный на рисунке 56.2. Скручивающаяся спираль получается вследствие того, что при увеличении номера кольца амплитуда волны немного уменьшается. Результирующее колебание изображается векторной суммой элементарных векторов. Элементарные волны, приходящие от некоторой зоны Френеля, лежат на полувитке спирали, причем нечетным зонам соответствуют правые части витка, а четным – левые.

Из векторной диаграммы видно, что амплитуды волн, приходящих от смежных зон Френеля, примерно равны, но отличаются по фазе на 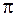. Амплитуда результирующего колебания (и соответственно интенсивность) в центре картины имеет максимальное значение, если число зон 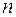нечетное, и минимальное значение при четном числе зон, укладывающихся в отверстии. При большом числе зон Френеля (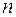>>1) амплитуда результирующей волны в 2 раза меньше амплитуды волны от первой зоны (рис. 56.2, г).

При увеличении диаметра отверстия или по мере приближения точки наблюдения () число зон Френеля, укладывающихся в пределах отверстия, будет возрастать. В обоих случаях интенсивность света будет периодически изменяться, принимая поочередно минимальные и максимальные значения в зависимости от числа зон Френеля. Так как при возрастании номера зоны 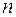амплитуда 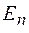уменьшается, то максимумы и минимумы интенсивности постепенно приближаются к интенсивности 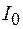при полностью открытом волновом фронте. На рисунке 56.3 показан график зависимости интенсивности света в центре картины от расстояния 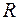до отверстия.

Если в отверстии установить пластинку, у которой все четные зоны Френеля сделаны непрозрачными, то волны от нечетных зон, прошедшие через пластинку, будут складываться в точке наблюдения в одинаковой фазе, что приведет к резкому возрастанию интенсивности света. Такую пластинку называют зонной пластинкой Френеля, и она работает подобно фокусирующей линзе. Еще большего эффекта можно добиться, если сделать так, чтобы в пределах четных зон пластинка вносила дополнительную разность хода . В этом случае волны от всех зон Френеля будут приходить в фазе и в результате интерференции усиливать друг друга, что приведет к еще большему возрастанию интенсивности. Такой оптический элемент называют фазовой пластинкой Френеля.

Картину дифракции Фраунгофера можно наблюдать на большом расстоянии от круглого отверстия (в дальней зоне). В этом случае размеры отверстия меньше радиуса первой зоны Френеля. В центре картины всегда наблюдается светлое пятно, в котором сосредоточено 84 % светового потока, прошедшего через отверстие. Первый дифракционный минимум наблюдается под углом

, (56.1)

и соответственно радиус первого темного кольца равен .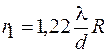

Дифракция Фраунгофера на круглом отверстии имеет большое практическое значение, поскольку большинство оптических приборов имеют круглые оправы. Представим, что с помощью оптического прибора (например, телескопа) наблюдаются две близко расположенные звезды, которые можно рассматривать как точечные объекты. В результате дифракции изображение каждой звезды будет представлять собой не точку, а размытое пятно, как на рисунке 56.1. Если звезды расположены достаточно близко друг к другу, то их изображения сольются, и наблюдатель не сможет различить их как два разных объекта. Таким образом, явление дифракции устанавливает теоретический предел разрешающей способности оптических приборов. Для объективной оценки разрешающей способности используют критерий Рэлея, согласно которому два точечных объекта считаются разрешаемыми, если центральный максимум дифракционной картины одного из них совпадает с первым дифракционным минимумом другого. В соответствии с критерием Рэлея угловая разрешающая способность оптического прибора с круглой апертурой определяется выражением (56.1).

В видимом диапазоне длин волн (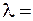0,5 мкм, что соответствует зеленому цвету, для которого глаз имеет максимальную чувствительность) для невооруженного глаза, полагая диаметр зрачка , разрешающая способность составит 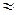30 угл. с. При наблюдении в полевой бинокль, имеющий диаметр объектива , из выражения (56.1) получим А для астрономического телескопа с диаметром главного зеркала 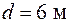разрешающая способность равна 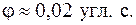Как видно из этих оценок, применение оптических приборов существенно увеличивает разрешающую способность глаза.

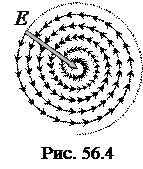Метод зон Френеля и векторная диаграмма позволяют объяснить кажущийся парадокс, который явился одним из решающих доказательств правильности представлений о волновой природе света. Если на пути плоской волны вместо экрана с отверстием поставить непрозрачный диск, то он перекроет часть волновой поверхности. Векторная диаграмма будет иметь вид, показанный на рисунке 56.4, где пунктиром изображены элементарные векторы амплитуд, соответствующие перекрытой части волновой поверхности. Амплитуда результирующего колебания изобразится вектором , проведенным из начала "урезанной" спирали к ее центру. При увеличении размера диска амплитуда (и интенсивность) будет уменьшаться, тем не менее, она всегда отлична от нуля. Это означает, что в центре за непрозрачным диском всегда должно наблюдаться светлое пятно. Французский физик и математик Симеон Дени Пуассон на основе работ Френеля первым пришел к этому на первый взгляд нелепому выводу и посчитал его доказательством ошибочности теории Френеля. Однако вскоре французский физик и астроном Доминик Араго действительно обнаружил светлое пятно в центре геометрической тени диска, и после этого волновая теория света стала общепризнанной.

Дата добавления: 2014-01-05