
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЧАСТЬ II. Специальная теория относительности
|
|
|
|
2.1. Принцип относительности Галилея и электродинамика.
В классической механике вводится понятие инерциальной системы отсчета как системы, в которой законы механики имеют наиболее простой вид. Например, уравнения движения системы материальных точек в инерциальной системе отсчета будут следующими:

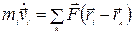 . (1.1)
. (1.1)
Рассмотрим инерциальную систему отсчета К и другую систему К', движущуюся поступательно со скоростью 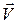 относительно первой. Две системы координат связаны между собой преобразованием Галилея:
относительно первой. Две системы координат связаны между собой преобразованием Галилея:
 (1.2)
(1.2)
или
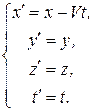 (1.3)
(1.3)
В классической механике постулируется абсолютный характер времени, что отражено в последнем равенстве (1.3). Из преобразований Галилея следует классический закон сложения скоростей
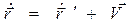 (1.4)
(1.4)
и закон для ускорений
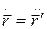 . (1.5)
. (1.5)
Уравнения движения системы материальных точек в системе отсчета К' могут быть получены из (1.1) с учетом (1.4) и (1.5) в виде:
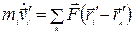 . (1.6)
. (1.6)
Таким образом, уравнения движения при преобразованиях Галилея не меняют вид и система отсчета К' также будет инерциальной. Отсюда следует, что существует бесконечно много инерциальных систем отсчета, совершающих
равномерное и прямолинейное движение или покоящихся друг относительно друга. В этих системах законы механики выполняются в простой классической форме.
Следовательно, находясь внутри инерциальной системы отсчета и проводя механические опыты, нельзя определить, движется эта система отсчета прямолинейно и равномерно или покоится. Это есть одна из формулировок известного принципа относительности Галилея. Другая формулировка этого принципа заключается в том, что уравнения механики во всех инерциальных системах отсчета имеют одинаковый вид, и значит, они инвариантны относительно преобразований Галилея. С точки зрения классической механики все инерциальные системы отсчета равноправны.
|
|
|
Однако уравнения Максвелла оказываются неинвариантными относительно преобразований Галилея. Решая уравнения Максвелла для излучателя, найдем в волновой зоне  . Волновой фронт в момент времени
. Волновой фронт в момент времени  определяется уравнением
определяется уравнением  или
или  . Перейдем в другую инерциальную систему отсчета с помощью преобразований Галилея и получим новое уравнение для волнового фронта
. Перейдем в другую инерциальную систему отсчета с помощью преобразований Галилея и получим новое уравнение для волнового фронта  . Вид уравнений, определяющий волновой фронт в новой инерциальной системе отсчета отличается от исходного и поэтому можно определить скорость
. Вид уравнений, определяющий волновой фронт в новой инерциальной системе отсчета отличается от исходного и поэтому можно определить скорость 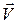 новой системы отсчета К' относительно системы К.
новой системы отсчета К' относительно системы К.
Скорость света  измеряется относительно некоторой гипотетической среды, называемой мировым эфиром. Уравнения Максвелла справедливы в системе отсчета, связанной с мировым эфиром. Тогда скорость
измеряется относительно некоторой гипотетической среды, называемой мировым эфиром. Уравнения Максвелла справедливы в системе отсчета, связанной с мировым эфиром. Тогда скорость 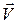 есть скорость подвижной системы отсчета относительно мирового эфира и ее часто называют абсолютной скоростью. Попытки обнаружения движения относительно мирового эфира (эфирного ветра) предпринимались еще до создания теории электромагнетизма. Опыты Араго, Физо, Хека, Маскарта, Майкельсона и Морли показали, что обнаружить эфирный ветер не удается как в опытах первого порядка по
есть скорость подвижной системы отсчета относительно мирового эфира и ее часто называют абсолютной скоростью. Попытки обнаружения движения относительно мирового эфира (эфирного ветра) предпринимались еще до создания теории электромагнетизма. Опыты Араго, Физо, Хека, Маскарта, Майкельсона и Морли показали, что обнаружить эфирный ветер не удается как в опытах первого порядка по  (Араго, Физо, Хек, Маскарт), так и в опытах второго порядка по
(Араго, Физо, Хек, Маскарт), так и в опытах второго порядка по  (Майкельсон и Морли).
(Майкельсон и Морли).
Возможны три варианта построения физической теории:
1) Принцип относительности применим только в механике и не применим к электродинамике. Отсюда следует, что должна существовать преимущественная система отсчета (мировой эфир). Однако этот путь был окончательно отвергнут опытами Майкельсона и Морли.
2) Принцип относительности применим как в механике, так и в электродинамике. При этом необходимо считать, что уравнения Максвелла неверны и должны быть заменены новыми. Однако попытки найти отклонения от законов классической электродинамики оказались безуспешными.
|
|
|
3) Принцип относительности применим в механике и в электродинамике, но законы механики необходимо исправить. Таким образом, новая теория должна была установить границы применимости классической ньютоновой механики. Поэтому очень важным были бы опыты, в которых наблюдались отклонения от законов классической механики.
Третий путь построения физической теории оказался единственным продуктивным путем. В работах Лоренца, Пуанкаре, Эйнштейна были заложены основы новой физической теории - специальной теории относительности (СТО).
2.2. Постулаты специальной теории относительности. Преобразования Лоренца.
Специальная теория относительности базируется на двух постулатах.
1) Принцип относительности.
Все механические и электромагнитные процессы в инерциальных системах отсчета протекают одинаково.
Т.е. уравнения Максвелла и модифицированные законы механики во всех инерциальных системах отсчета должны иметь одинаковый вид.
2) Принцип постоянства скорости света.
Скорость света во всех инерциальных системах одинакова и не зависит от скорости движения источника света.
Найдем закон преобразования координат и времени при переходе из одной инерциальной системы отсчета в другую. Пусть  . Искомое преобразование
. Искомое преобразование

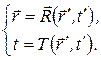 (2.1)
(2.1)
Обратное преобразование
 (2.2)
(2.2)
Здесь предполагается, что время в разных системах отсчета протекает неодинаково в отличие от классической механике.
Пусть в некоторый момент времени 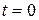 начала координат обеих систем отсчета совпадало и в этот момент времени из начала координат излучается сферическая электромагнитная (световая) волна. Уравнения волновых поверхностей в системе отсчета К и К' имеют вид
начала координат обеих систем отсчета совпадало и в этот момент времени из начала координат излучается сферическая электромагнитная (световая) волна. Уравнения волновых поверхностей в системе отсчета К и К' имеют вид
 (2.3)
(2.3)
где  и
и  - пространственно - временные прямое и обратное преобразования. При записи уравнений (2.3) были использованы оба постулата теории относительности. Вначале рассмотрим преобразования Галилея
- пространственно - временные прямое и обратное преобразования. При записи уравнений (2.3) были использованы оба постулата теории относительности. Вначале рассмотрим преобразования Галилея
 (2.4)
(2.4)
Тогда

=  ,
, 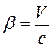 .
.
Отсюда следует, что преобразования Галилея не являются преобразованиями, которые с точки зрения электродинамики связывают инерциальные системы отсчета.
Проведем диагонализацию квадратичной формы, выделив полный квадрат:
|
|
|
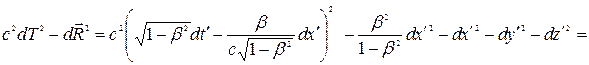
= .
.
Введем обозначения
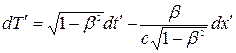 ,
,  ,
, 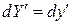 ,
, 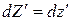 ,
,
или
 ,
,  ,
,  ,
, 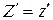 . (2.5)
. (2.5)
Из (2.4) следует
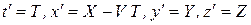 . (2.6)
. (2.6)
Подставим эти значения в (2.5) и получим
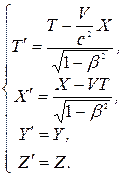 (2.7)
(2.7)
С учетом введенных обозначений, получим преобразования

 (2.8)
(2.8)
которые называют преобразованиями Лоренца. Очевидно, что 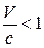 или
или  . Это означает, что скорости тел не могут превышать скорости света в вакууме. В случае, когда
. Это означает, что скорости тел не могут превышать скорости света в вакууме. В случае, когда 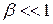 или
или  , преобразования Лоренца совпадают с преобразованиями Галилея.
, преобразования Лоренца совпадают с преобразованиями Галилея.
2.3. Преобразования отрезков и промежутков времени. Интервал.
 Пусть в системе отсчета К' покоится отрезок длины
Пусть в системе отсчета К' покоится отрезок длины  , которую принято называть собственной длиной отрезка (масштаба). Воспользуемся преобразованиями Лоренца и получим
, которую принято называть собственной длиной отрезка (масштаба). Воспользуемся преобразованиями Лоренца и получим

 .
.
В системе К измерения начала и конца масштаба должно быть проведено одновременно, т.е. 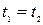 . Тогда длина масштаба в системе К будет
. Тогда длина масштаба в системе К будет  . Окончательно получим
. Окончательно получим
 . (3.1)
. (3.1)
Такое сокращение длины масштаба называют лоренцевым сокращением. В поперечном направлении не происходит изменение размеров масштаба, т.е. сечение масштаба не изменяется. Найдем элементарный объем движущегося вдоль оси 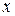 масштаба
масштаба
 ,
,
или
 . (3.2)
. (3.2)
Таким образом, объем движущегося тела уменьшается.
Рассмотрим, как изменяются промежутки времени между двумя физическими событиями при переходе из системы отсчета К в систему К'. Предположим, что два события произошли одновременно в системе отсчета К. При этом предполагается, что они произошли в разных точках пространства, т.е.  ,
,  . Тогда
. Тогда
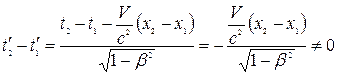 .
.
Следовательно, события одновременные в одной системе отсчета не будут одновременными и другой системе отсчета.
Пусть в некоторой точке подвижной системы отсчета К' произошли два события с промежутком времени  .Найдем промежуток времени между этими событиями в системе отсчета К
.Найдем промежуток времени между этими событиями в системе отсчета К
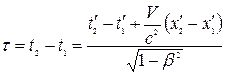 .
.
Так как  , то
, то
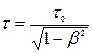 . (3.3)
. (3.3)
Отсюда следует, что  , т.е. движущиеся часы замедляют свой ход.
, т.е. движущиеся часы замедляют свой ход.
Таким образом, ни промежутки времени, ни пространственные интервалы не являются инвариантами при преобразованиях Лоренца. Следовательно, теория относительности требует введения вместо трехмерного евклидового пространства нового четырехмерного пространства - времени, которое является псевдоевклидовым. К трем пространственным координатам
|
|
|
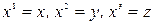 добавляют четвертую координату
добавляют четвертую координату  . Можно показать, что при преобразованиях Лоренца элементарный четырехмерный объем будет инвариантом. Действительно,
. Можно показать, что при преобразованиях Лоренца элементарный четырехмерный объем будет инвариантом. Действительно,
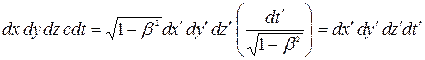 .
.
Введем в четырехмерном псевдоевклидовом пространстве – времени интервал как обобщение обычного пространственного интервала (расстояния) между двумя точками и временного интервала (промежутка времени) между двумя событиями. Квадрат интервала:
 . (3.4)
. (3.4)
Эта величина инвариантна относительно преобразования Лоренца, т.е.
 . (3.5)
. (3.5)
Интервал между двумя бесконечно близкими событиями
 ,
,
где  - скорость движения частицы. В системе отсчета, где частица покоится,
- скорость движения частицы. В системе отсчета, где частица покоится,  и
и  . Введем
. Введем
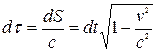 (3.6)
(3.6)
- собственное время. Оно также является инвариантом.
Интервалы бывают трех типов.
· Времениподобный интервал - интервал между событиями, для которого 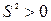 .
.
· Пространственноподобный интервал - интервал между событиями, для которого  .
.
· Нулевой (светоподобный) интервал – интервал между событиями, для которого 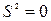 . Световая скорость – максимальная (предельная) скорость распространения сигналов и условие
. Световая скорость – максимальная (предельная) скорость распространения сигналов и условие 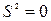 - просто уравнение распространения световой волны.
- просто уравнение распространения световой волны.
Пусть имеют место два события, для которых в системе отсчета К время 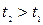 и
и 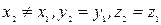 . Найдем промежуток времени между этими событиями в системе K'
. Найдем промежуток времени между этими событиями в системе K'
 . (3.7)
. (3.7)
В системе K промежуток времени между событиями будет - 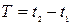 , расстояние -
, расстояние - 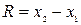 . Если первое событие причина, а второе – следствие, то порядок следования событий не должен изменится, т.е.
. Если первое событие причина, а второе – следствие, то порядок следования событий не должен изменится, т.е.  и
и  . Тогда из (3.7) следует
. Тогда из (3.7) следует  . С учетом того, что
. С учетом того, что 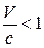 , получим
, получим 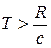 . Это означает, что время прохождения светового сигнала
. Это означает, что время прохождения светового сигнала  между точками
между точками  и
и 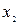 не превышает временной промежуток
не превышает временной промежуток  между этими событиями. Действительно, предельная скорость передачи информации равна скорости света в вакууме
между этими событиями. Действительно, предельная скорость передачи информации равна скорости света в вакууме  . Если выполняется условие
. Если выполняется условие  , то такие события не могут быть связаны причинно – следственной связью. Иначе получим из (3.7), что меняется порядок следования событий. Т.е. если
, то такие события не могут быть связаны причинно – следственной связью. Иначе получим из (3.7), что меняется порядок следования событий. Т.е. если  в системе К, то
в системе К, то  в системе K'. Тогда
в системе K'. Тогда 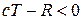 или
или 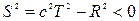 . Интервал между такими событиями пространственноподобный.
. Интервал между такими событиями пространственноподобный.
Таким образом, два события, разделенные пространственноподобным интервалом, не могут быть связаны причинно - следственной связью. Если два события, связанные пространственноподобным интервалом, одновременны в системе К, то  и они разделены в пространстве.
и они разделены в пространстве.
Для событий, связанных причинно - следственной связью, выполняется условие 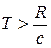 или
или 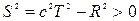 . Такие события разделены времениподобным интервалом.
. Такие события разделены времениподобным интервалом.
Следовательно, только два события, разделенные времениподобным интервалом, могут быть связаны причинно - следственной связью.
Можно показать, что неодноместные события, связанные времениподобным интервалом, не могут быть одновременными. Положим  . Тогда получим
. Тогда получим  .
.
2.4. Релятивистский закон сложения скоростей. Закон преобразования углов.
Рассмотрим частицу с координатами  в момент времени
в момент времени  . Ее скорость в системе отсчета К:
. Ее скорость в системе отсчета К:

 .
.
В системе отсчета К':
 .
.
Воспользовавшись преобразованиями Лоренца (2.6), получим
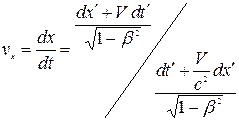 =
= 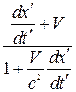
или
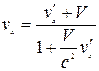 . (4.1)
. (4.1)
Аналогично найдем
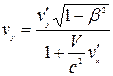 , (4.2)
, (4.2)
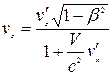 . (4.3)
. (4.3)
В нерелятивистском случае, когда  , получим из (4.1) - (4.3)
, получим из (4.1) - (4.3)
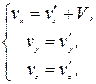 (4.4)
(4.4)
т.е. обычный классический закон сложения скоростей. Следует отметить, что классический закон сложения скоростей отвечает обычному правилу сложения векторов в евклидовом пространстве. Релятивистский же закон сложения скоростей в специальной теории относительности совпадает с правилом сложения скоростей в геометрии Лобачевского.
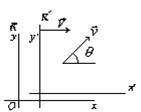 Рассмотрим закон преобразования углов в специальной теории относительности. Пусть частица движется в системе отсчета К со скоростью
Рассмотрим закон преобразования углов в специальной теории относительности. Пусть частица движется в системе отсчета К со скоростью 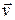 , под углом
, под углом  к оси
к оси 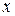 . При этом считаем, что
. При этом считаем, что  . Тогда имеем
. Тогда имеем
 (4.5)
(4.5)
Отсюда, с учетом закона сложения скоростей в специальной теории относительности, найдем
 . (4.6)
. (4.6)
Для случая, когда  , отсюда получим
, отсюда получим
 . (4.7)
. (4.7)
Если частица – фотон и  , то из (4.7) следует формула
, то из (4.7) следует формула
 , (4.8)
, (4.8)
объясняющая явление астрономической аберрации (аберрации света).
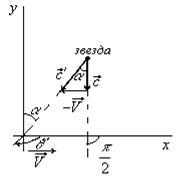 Брадлей (Брэдли) в 1728 году заметил, что положение звезды
Брадлей (Брэдли) в 1728 году заметил, что положение звезды  Дракона меняется в течение года. Он понял, что явление аберрации обусловлено движением Земли по орбите и конечностью скорости света. Исходя из ньютоновой корпускулярной теории света, Брадлей дал объяснение этому эффекту. Скорость света относительно Земли
Дракона меняется в течение года. Он понял, что явление аберрации обусловлено движением Земли по орбите и конечностью скорости света. Исходя из ньютоновой корпускулярной теории света, Брадлей дал объяснение этому эффекту. Скорость света относительно Земли  , где
, где 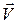 - скорость Земли относительно Земли. Отсюда получим
- скорость Земли относительно Земли. Отсюда получим
 . (4.9)
. (4.9)
 В 1804 году Юнг дал объяснение этому явлению с точки зрения волновой теории, предполагая, что эфир не увлекается Землей. Волны, прошедшие через диафрагму (объектив телескопа) и распространяющиеся в неувлекаемом Землей эфире, попадут левее того места AB, куда бы они пришли в случае неподвижной Земли. При полном увлечении эфира волны попадают на отрезок AB, как и в случае неподвижной относительно эфира Земли.
В 1804 году Юнг дал объяснение этому явлению с точки зрения волновой теории, предполагая, что эфир не увлекается Землей. Волны, прошедшие через диафрагму (объектив телескопа) и распространяющиеся в неувлекаемом Землей эфире, попадут левее того места AB, куда бы они пришли в случае неподвижной Земли. При полном увлечении эфира волны попадают на отрезок AB, как и в случае неподвижной относительно эфира Земли.
Объяснение с точки зрения специальной теории относительности простое. Воспользуемся формулой (4.8). Положим угол 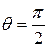 в неподвижной системе отсчета, связанной со звездой. В системе, связанной с Землей, угол
в неподвижной системе отсчета, связанной со звездой. В системе, связанной с Землей, угол  . Тогда получим классическую формулу для аберрации света:
. Тогда получим классическую формулу для аберрации света: 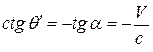 или
или  .
.
В 1851 году был поставлен опыт Физо по определению увлечения эфира движущимися телами. Такое увлечение эфира телами было в виде гипотезы предложено Френелем для объяснения опыта Араго. Так как изменяется показатель преломления тела в зависимости от скорости движения его к источнику света или от него, то изменяется показатель преломления призмы в случае неувлекаемого эфира и, следовательно, угол отклонения луча призмой. Ожидаемое значение угла отклонения луча должно было составить 1'. Также изменяется фокусное расстояние линзы. Однако Араго не получил в своих опытах предсказанного теорией неувлекаемого эфира эффекта.
Френель показал, что для объяснения отрицательного результата опытов Араго необходимо предположить, что эфир частично увлекаем. Если тело движется со скоростью 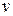 , то с такой же скоростью его обтекает эфир (эфирный ветер). Френель показал, что внутри вещества вследствие частичного увлечения эфира скорость эфирного ветра уменьшается до значения
, то с такой же скоростью его обтекает эфир (эфирный ветер). Френель показал, что внутри вещества вследствие частичного увлечения эфира скорость эфирного ветра уменьшается до значения  . Разность скоростей
. Разность скоростей 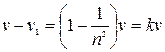 , где
, где 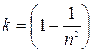 - френелевский коэффициент увлечения эфира. Так как опыты Араго не обладали достаточной точностью, то Физо поставил опыт по определению
- френелевский коэффициент увлечения эфира. Так как опыты Араго не обладали достаточной точностью, то Физо поставил опыт по определению 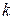 коэффициента увлечения эфира. В случае
коэффициента увлечения эфира. В случае  - эфир не увлекается телом,
- эфир не увлекается телом,  - увлекается полностью,
- увлекается полностью, 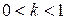 - увлекается частично. Найденный Физо коэффициент совпал в точности с френелевским коэффициентом увлечения
- увлекается частично. Найденный Физо коэффициент совпал в точности с френелевским коэффициентом увлечения 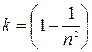 . Пусть скорость света в покоящейся среде
. Пусть скорость света в покоящейся среде  . Тогда скорость света в движущейся среде в случае неувлекаемого эфира согласно классическому закону сложения скоростей будет
. Тогда скорость света в движущейся среде в случае неувлекаемого эфира согласно классическому закону сложения скоростей будет  . В опыте Физо оказалось, что эта скорость
. В опыте Физо оказалось, что эта скорость  . Это интерпретировалось, как увлечение эфира движущейся средой.
. Это интерпретировалось, как увлечение эфира движущейся средой.
Специальная теория относительности дала другое объяснение опыту Физо. В этом опыте впервые было замечено отклонение от классического закона сложения скоростей. Воспользуемся законом сложения скоростей (4.1). Тогда
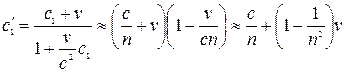 . (4.10)
. (4.10)
При выводе были отброшены члены первого и более высоких порядков по  . Таким образом, опыт Физо является экспериментальным подтверждением формулы сложения скоростей специальной теории относительности.
. Таким образом, опыт Физо является экспериментальным подтверждением формулы сложения скоростей специальной теории относительности.
До создания теории относительности казалось, что опыты по определению эфирного ветра дадут возможность определить скорость движения тела относительно эфира. Можно строго доказать, что вытекающее из формулы Френеля частичное увлечение эфира, автоматически компенсирует в первом порядке по 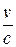 эффект эфирного ветра и делает невозможной задачу определения абсолютного движения в экспериментах первого порядка по
эффект эфирного ветра и делает невозможной задачу определения абсолютного движения в экспериментах первого порядка по 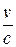 . Поэтому необходимы были опыты по определению эфирного ветра во втором порядке по
. Поэтому необходимы были опыты по определению эфирного ветра во втором порядке по 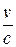 . Такие опыты были поставлены Майкельсоном (1981 год) и им же совместно с Морли (1887 год). В этих опытах также не был обнаружен эфирный ветер, хотя точность эксперимента была таковой, что без труда позволяла бы это сделать. Опыты Майкельсона и Морли показали, что скорость света в вакууме остается постоянной и не зависит от скорости движения источника света и скорости наблюдателя. Различные попытки объяснения отрицательного результата опытов Майкельсона и Морли на основе классических представлений о мировом эфире оказались безуспешными. Только теория относительности, взяв в качестве одного из постулатов принцип постоянства скорости света, была в состоянии объяснить все проводимые в этой области физики эксперименты. Выводы теории относительности хорошо подтверждались в многочисленных экспериментах по ее проверке.
. Такие опыты были поставлены Майкельсоном (1981 год) и им же совместно с Морли (1887 год). В этих опытах также не был обнаружен эфирный ветер, хотя точность эксперимента была таковой, что без труда позволяла бы это сделать. Опыты Майкельсона и Морли показали, что скорость света в вакууме остается постоянной и не зависит от скорости движения источника света и скорости наблюдателя. Различные попытки объяснения отрицательного результата опытов Майкельсона и Морли на основе классических представлений о мировом эфире оказались безуспешными. Только теория относительности, взяв в качестве одного из постулатов принцип постоянства скорости света, была в состоянии объяснить все проводимые в этой области физики эксперименты. Выводы теории относительности хорошо подтверждались в многочисленных экспериментах по ее проверке.
2.5. Элементы тензорной алгебры. Ковариантная запись дифференциального закона сохранения заряда. Законы преобразования плотностей заряда и тока.
Специальная теория относительности установила инвариантность интервала  при переходе из одной инерциальной системы отсчета в другую, т.е. инвариантность интервала при преобразованиях Лоренца. Впервые Пуанкаре, а затем Минковский показали, что обычное трехмерное пространство и время представляют собой единое четырехмерное пространство – время. О точках такого пространства говорят как о физических событиях. Радиус – вектор любой точки (события) пространства- времени имеет четыре компоненты и его можно записать в виде
при переходе из одной инерциальной системы отсчета в другую, т.е. инвариантность интервала при преобразованиях Лоренца. Впервые Пуанкаре, а затем Минковский показали, что обычное трехмерное пространство и время представляют собой единое четырехмерное пространство – время. О точках такого пространства говорят как о физических событиях. Радиус – вектор любой точки (события) пространства- времени имеет четыре компоненты и его можно записать в виде
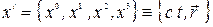 , (5.1)
, (5.1)
где  - трехмерный радиус – вектор. Таким образом, в четырехмерном пространстве введем четыре взаимно ортогональные координатные оси
- трехмерный радиус – вектор. Таким образом, в четырехмерном пространстве введем четыре взаимно ортогональные координатные оси 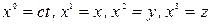 .
.
Рассмотрим закон преобразования координат при переходе из одной системы отсчета в другую. При этом не ограничиваемся только инерциальными системами отсчета. Закон преобразования координат запишем в виде:
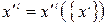 . (5.2)
. (5.2)
Это преобразование должно быть не вырожденным, чтобы имело место обратное преобразование
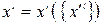 . (5.3)
. (5.3)
Следовательно, якобиан преобразования
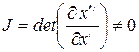 .
.
Рассмотрим малое перемещение в четырехмерном пространстве:
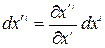 . (5.4)
. (5.4)
Здесь применено известное правило суммирования Эйнштейна, согласно которому по повторяющимся (немым) индексам производится суммирование. Малое перемещение 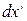 в четырехмерном пространстве обобщает перемещение
в четырехмерном пространстве обобщает перемещение 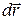 в трехмерном пространстве,
в трехмерном пространстве, 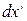 - контрвариантный вектор в четырехмерном пространстве.
- контрвариантный вектор в четырехмерном пространстве.
Обобщая правило преобразования четырехмерного вектора перемещения (5.4), введем произвольный четырехмерный контрвариантный вектор 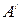 , который преобразуется при заданном законе преобразования координат (5.2) по следующему правилу
, который преобразуется при заданном законе преобразования координат (5.2) по следующему правилу
 , (5.5)
, (5.5)
где  .
.
Пусть 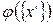 - произвольная скалярная функция. Тогда
- произвольная скалярная функция. Тогда
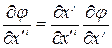 .
.
Введем 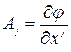 - ковариантный вектор. Получим правило преобразования ковариантных векторов при переходе из одной системы координат в другую:
- ковариантный вектор. Получим правило преобразования ковариантных векторов при переходе из одной системы координат в другую:
 . (5.6)
. (5.6)
Можно обобщить понятие скаляра на четырехмерное пространство:
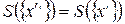 .
.
В частности, четырехмерный интервал
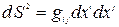 ,
,  (5.7)
(5.7)
есть пример четырехмерной скалярной функции. Здесь  - ковариантный метрический тензор в произвольных координатах. Такая запись интервала обобщает вид интервала в декартовых координатах инерциальной системы отсчета
- ковариантный метрический тензор в произвольных координатах. Такая запись интервала обобщает вид интервала в декартовых координатах инерциальной системы отсчета
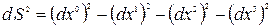 , (5.8)
, (5.8)
для которых метрический тензор

имеет диагональный вид. Согласно (5.7) в произвольных координатах имеем 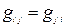 .
.
Найдем закон преобразования метрического тензора при переходе из одной системы координат в другую:
 .
.
Следовательно, получим
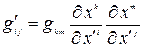 . (5.9)
. (5.9)
Рассматриваемый метрический тензор – ковариантный тензор второго ранга.
Для матрицы  построим обратную матрицу
построим обратную матрицу  , которая удовлетворяет условию
, которая удовлетворяет условию  . Матрица
. Матрица  определяет контрвариантный метрический тензор второго ранга. Найдем закон преобразования для этого тензора:
определяет контрвариантный метрический тензор второго ранга. Найдем закон преобразования для этого тензора:
 ,
,
где
 .
.
Тогда
 . (5.10)
. (5.10)
Можно ввести контрвариантный тензор произвольного ранга  , который удовлетворяет следующему закону преобразования при переходе из одной системы координат в другую:
, который удовлетворяет следующему закону преобразования при переходе из одной системы координат в другую:
 . (5.11)
. (5.11)
Аналогично введем ковариантный тензор ранга 
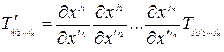 . (5.12)
. (5.12)
С помощью метрического тензора можно опускать и поднимать индексы у тензоров. Например:
 .
.
В инерциальной системе отсчета метрический тензор
 .
.
Действительно, так как
 и
и 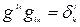 ,
,
то  при
при  ,
, 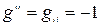 при
при 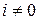 и
и 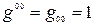 .
.
Введем ковариантный вектор перемещения  . Если определить скалярное произведение векторов следующим образом:
. Если определить скалярное произведение векторов следующим образом: 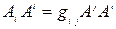 , то
, то
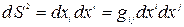 .
.
Запись физических выражений в четырехмерном тензорном виде называют ковариантной записью физических уравнений. При такой форме записи вид выражений не меняется при преобразованиях Лоренца. Следовательно, законы физики должны быть записаны в ковариантном виде.
Вначале рассмотрим закон сохранения заряда
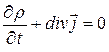
и перепишем его в ковариантной форме. Введем 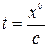 . Тогда
. Тогда
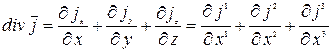 ,
,  .
.
Введем  . Если ввести четырехмерный вектор тока
. Если ввести четырехмерный вектор тока 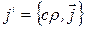 , то закон сохранения заряда может быть записан в ковариантной форме
, то закон сохранения заряда может быть записан в ковариантной форме
 . (5.13)
. (5.13)
Найдем закон преобразования четырехмерного вектора тока
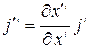 . (5.14)
. (5.14)
Воспользуемся преобразованиями Лоренца
 или
или 
где 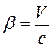 ,
,  . Отсюда следует, что
. Отсюда следует, что
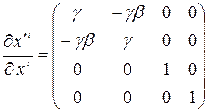 . (5.15)
. (5.15)
Положив в (5.14)  , получим
, получим

или
 . (5.16)
. (5.16)
Взяв 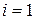 , получим:
, получим:
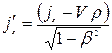 . (5.17)
. (5.17)
При 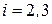 :
: 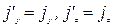 .
.
Таким образом, преобразования четырехмерного тока 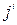 :
:
 (5.18)
(5.18)
Обратное преобразование
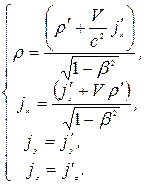 (5.19)
(5.19)
Пусть заряды покоятся в инерциальной системе отсчета К', т.е. 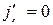 ,
, 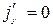 ,
,  . Тогда
. Тогда
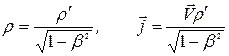 .
.
Воспользуемся законом преобразования объема 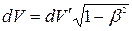 и найдем, как преобразуется заряд
и найдем, как преобразуется заряд 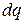 в объеме
в объеме  . Получим
. Получим
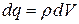 =
=  =
= 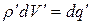 .
.
Это означает, что заряд любого элемента объема есть инвариант при преобразованиях Лоренца, т.е. при переходе из одной инерциальной системы отсчета в другую.
2.6. Ковариантная запись условия Лоренца и уравнений для потенциала. Закон преобразования потенциалов.
Перепишем условие Лоренца
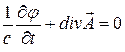
в виде
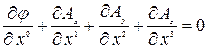 .
.
Введем четырехмерный контравариантный вектор потенциала 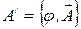 , где
, где  ,
, 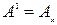 ,
,  ,
,  . Ковариантный вектор потенциала
. Ковариантный вектор потенциала  . При этом условие Лоренца в ковариантном виде
. При этом условие Лоренца в ковариантном виде
 . (6.1)
. (6.1)
Закон преобразования потенциалов
 (6.2)
(6.2)
запишем в виде
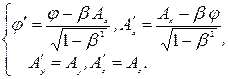 (6.3)
(6.3)
Уравнение для потенциалов
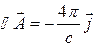 ,
, 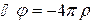 , (6.4)
, (6.4)
где оператор Даламбера
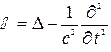
или
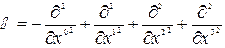 =
=  =
=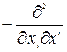 . (6.5)
. (6.5)
Тогда уравнения для потенциалов (6.4) перепишем в виде
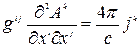 (6.6)
(6.6)
или
 . (6.7)
. (6.7)
2.7. Тензор электромагнитного поля. Ковариантная запись уравнений Максвелла для полей в вакууме.
Уравнения Максвелла также могут быть записаны в ковариантном виде. Для этого введем тензор электромагнитного поля. Напряженности электромагнитного поля
 7.1)
7.1)
перепишем в координатном виде

 (7.2)
(7.2)
Введем координаты четырехмерного пространства 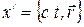 и четырехмерный ковариантный вектор потенциала
и четырехмерный ковариантный вектор потенциала 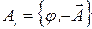 . Тогда соотношения (7.2) примут вид
. Тогда соотношения (7.2) примут вид
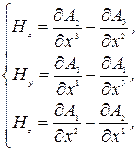
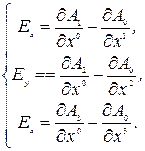 (7.3)
(7.3)
Рассмотрим тензор
 , (7.4)
, (7.4)
который называют тензором электромагнитного поля. Он является ковариантным, антисимметричным тензором второго ранга, т.е. для него выполняются следующие соотношения:
 .
.
Запишем тензор (7.4) в виде:
 . (7.5)
. (7.5)
Контрвариантный тензор электромагнитного поля
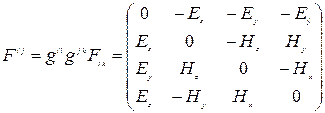 . (7.6)
. (7.6)
Запишем уравнения Максвелла в ковариантном виде, воспользовавшись введенным тензором электромагнитного поля. Рассмотрим уравнения Максвелла
 (7.7)
(7.7)
Уравнение  перепишем в виде:
перепишем в виде:
 , (7.8)
, (7.8)
где 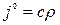 ,
,  . Уравнение
. Уравнение  преобразуем к виду:
преобразуем к виду:
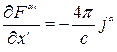 , (7.9)
, (7.9)
где 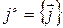 ,
, 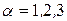 . Например, положив в (7.9)
. Например, положив в (7.9)  , получим
, получим
 ,
,
или
 .
.
Следовательно,
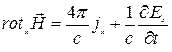 .
.
Таким образом, уравнения (7.8) и (7.9) можно записать в виде
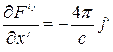 . (7.10)
. (7.10)
Преобразуем оставшуюся пару уравнений (7.7). Вначале рассмотрим
 .
.
Получим

или
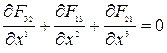 . (7.11)
. (7.11)
Аналогичным образом преобразуем уравнение  . В проекции на ось
. В проекции на ось 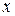 имеем
имеем

или
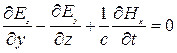 .
.
Окончательно получим
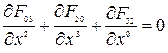 . (7.12)
. (7.12)
Таким образом, оставшуюся пару уравнений можно записать в виде
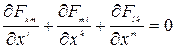 , (7.13)
, (7.13)
где 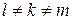 . Введем полностью антисимметричный тензор четвертого ранга
. Введем полностью антисимметричный тензор четвертого ранга  . Определим этот тензор следующим образом. Положим
. Определим этот тензор следующим образом. Положим  ,
,
 . Тензор
. Тензор  называют абсолютно антисимметричным тензором Леви – Чевиты. Четное число перестановок индексов
называют абсолютно антисимметричным тензором Леви – Чевиты. Четное число перестановок индексов  дает
дает
элементы этого тензора равные +1, а нечетное число перестановок индексов  дает элементы тензора равные -1. Всего ненулевых компонент тензора
дает элементы тензора равные -1. Всего ненулевых компонент тензора  будет 4!=4·3·2·1=24.
будет 4!=4·3·2·1=24.
Тогда уравнение (7.13) может быть переписано в виде
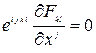 . (7.14)
. (7.14)
Тензор  - тензор третьего ранга, антисимметричный по всем трем индексам
- тензор третьего ранга, антисимметричный по всем трем индексам  ,
,  при условии
при условии 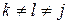 .
.
Таким образом, в ковариантной форме уравнения Максвелла:
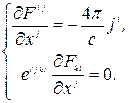 (7.15)
(7.15)
2.8. Законы преобразования напряженностей поля. Инварианты электромагнитного поля.
Запишем закон преобразования тензора электромагнитного поля:
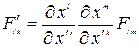 . (8.1)
. (8.1)
Здесь
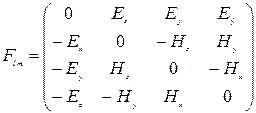 ,
, 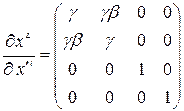 .
.
Положим в (8.1) 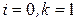 и получим
и получим
 =
= 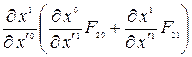 =
= =
=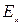 .
.
Аналогично можно получить законы преобразования других компонент напряженностей электромагнитного поля. Окончательно имеем
 (8.2)
(8.2)
Законы преобразования напряженностей электромагнитного поля можно записать в векторном виде. Рассмотрим параллельные и перпендикулярные к скорости 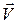 компоненты векторов напряженностей электромагнитного поля, т.е.
компоненты векторов напряженностей электромагнитного поля, т.е. 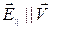 ,
, 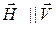 и
и  ,
,  . Тогда законы преобразования напряженностей (8.2) можно переписать в виде
. Тогда законы преобразования напряженностей (8.2) можно переписать в виде
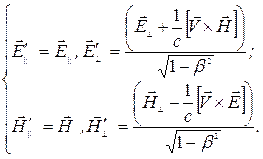 (8.3)
(8.3)
В нерелятивистском случае  эти формулы значительно упрощаются. С точностью до членов порядка
эти формулы значительно упрощаются. С точностью до членов порядка 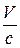 получим
получим
 (8.4)
(8.4)
Из компонент тензора электромагнитного поля 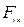 можно образовать следующие инварианты:
можно образовать следующие инварианты:
a) 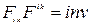 .
.
b) 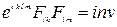
Выражая компоненты тензора электромагнитного поля 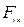 через компоненты
через компоненты 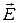 и
и  , можно показать, что эти инварианты имеют вид:
, можно показать, что эти инварианты имеют вид:
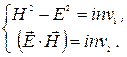 (8.5)
(8.5)
Можно было бы образовать еще один инвариант  . Но он тождественно обращается в нуль, т.е.
. Но он тождественно обращается в нуль, т.е.  .
.
Отметим, что первый инвариант истинный скаляр, т.е. он не изменяется как для поворотов в четырехмерном пространстве (преобразования Лоренца), так и относительно пространственных и временных отражений (преобразование инверсии). Второй инвариант псевдоскаляр. Он инвариант только для поворотов (преобразования Лоренца), но не инвариант для отражений.
Из (8.5) следует:
1) Если в какой–нибудь инерциальной системе отсчета 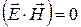 , т.е.
, т.е. 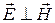 , то и в другой инерциальной системе отсчета
, то и в другой инерциальной системе отсчета  и значит
и значит  . Можно найти такую инерциальную систему отсчета, в которой либо
. Можно найти такую инерциальную систему отсчета, в которой либо  , если
, если  , либо
, либо  , если
, если 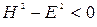 .
.
2) Если 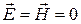 в какой – нибудь инерциальной системе отсчета, то они будут нулевыми во всех системах отсчета. Действительно,
в какой – нибудь инерциальной системе отсчета, то они будут нулевыми во всех системах отсчета. Действительно, 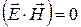 и
и 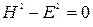 во всех инерциальных системах отсчета. Решение системы этих уравнений будет тривиальным:
во всех инерциальных системах отсчета. Решение системы этих уравнений будет тривиальным: 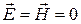 .
.
3) Если 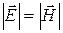 в какой–нибудь инерциальной системе отсчета, то
в какой–нибудь инерциальной системе отсчета, то  во всех системах отсчета.
во всех системах отсчета.
4) Если 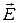 не перпендикулярно
не перпендикулярно  в какой – нибудь инерциальной системе отсчета, то можно найти такую систему отсчета, в которой
в какой – нибудь инерциальной системе отсчета, то можно найти такую систему отсчета, в которой  .
.
2.9. Инвариантность фазы. Законы преобразования частоты и волнового вектора электромагнитной волны. Астрономическая аберрация и эффект Доплера.
Рассмотрим плоскую электромагнитную волну в инерциальной системе отсчета К:
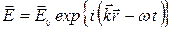 ,
,  . (9.1)
. (9.1)
В движущейся инерциальной системе отсчета К':
 ,
,  . (9.2)
. (9.2)
В системе отсчета К имеет место: 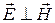 и
и 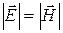 . Следовательно,
. Следовательно,
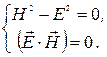 (9.3)
(9.3)
Такие же соотношения будут иметь место в движущейся инерциальной системе отсчета К':
 (9.4)
(9.4)
Так как 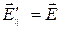 , то после подстановки значений из (9.1) и (9.2) получим:
, то после подстановки значений из (9.1) и (9.2) получим:
 ,
,
или
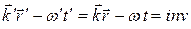 .
.
Таким образом, фаза волны 
 - инвариант. Амплитуды волны, согласно выражениям (8.3), преобразуются по следующим правилам:
- инвариант. Амплитуды волны, согласно выражениям (8.3), преобразуются по следующим правилам:
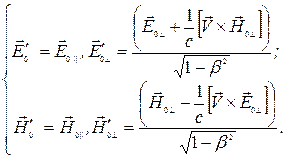 (9.5)
(9.5)
Введем четырехмерный контрвариантный волновой вектор  и ковариантный волновой вектор
и ковариантный волновой вектор  . Найдем
. Найдем
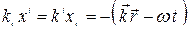 = inv, где
= inv, где  ,
, 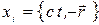 .
.
Следовательно,  и
и  действительно являются четырехмерными векторами.
действительно являются четырехмерными векторами.
Законы преобразования четырехмерного волнового вектора можно записать в матричном виде
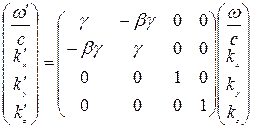 . (9.6)
. (9.6)
Отсюда получим
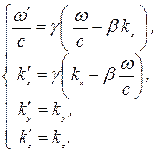 (9.7)
(9.7)
В уравнениях (9.7) заключено объяснение эффекта Доплера и явления звездной аберрации.
 Из волнового уравнения
Из волнового уравнения 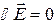 следует
следует 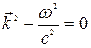 . Модуль волнового вектора
. Модуль волнового вектора  . Введем
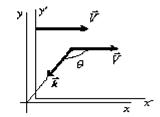
. Введем  . Источник света покоится в системе отсчета К', т.е. движется со скоростью
. Источник света покоится в системе отсчета К', т.е. движется со скоростью 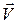 относительно системы К.
относительно системы К.
Считаем, что свет распространяется в плоскости  . Тогда из первого уравнения (9.7) получим
. Тогда из первого уравнения (9.7) получим
 , (9.8)
, (9.8)
или
 . (9.9)
. (9.9)
Выражение (9.9) описывает эффект Доплера. Если 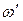 - частота движущегося вдоль
- частота движущегося вдоль 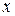 источника света, то
источника света, то 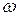 - частота света, воспринимаемого покоящимся наблюдателем.
- частота света, воспринимаемого покоящимся наблюдателем.
Если взять 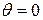 (источник света удаляется) или
(источник света удаляется) или  (источник света приближается), то из (9.9) получим
(источник света приближается), то из (9.9) получим
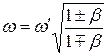 . (9.10)
. (9.10)
Эта формула описывает продольный эффект Доплера. В нерелятивистском случае получим известную формулу эффекта Доплера:
 . (9.11)
. (9.11)
Если взять 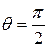 , то получим формулу для поперечного эффект Доплера
, то получим формулу для поперечного эффект Доплера
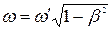 . (9.12)
. (9.12)
В нерелятивистском приближении 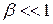 поперечный эффект Доплера отсутствует (
поперечный эффект Доплера отсутствует ( ). В 1938 году Айвс обнаружил релятивистский эффект Доплера, т.е. эффект второго порядка по
). В 1938 году Айвс обнаружил релятивистский эффект Доплера, т.е. эффект второго порядка по 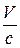 .
.
Из второго уравнения (9.7) получим
 .
.
Отсюда и из выражения (9.9) получим
 . (9.13)
. (9.13)
Согласно третьему уравнению (9.7) имеем
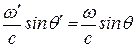 . (9.14)
. (9.14)
С учетом (9.9) получим
 . (9.15)
. (9.15)
Из (9.13) и (9.15) следует известная формула
 , (9.16)
, (9.16)
объясняющая эффект астрономической аберрации.
2.10. Релятивистское обобщение уравнений механики Ньютона. Уравнение движения заряженной релятивистской частицы во внешнем электромагнитном поле.
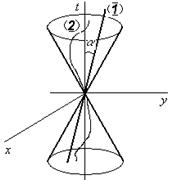 Рассмотрим движение частицы в пространстве Минковского (четырехмерное псевдоевклидово пространство – время). Частица описывает в четырехмерном пространстве кривую, которая называется мировой линией.
Рассмотрим движение частицы в пространстве Минковского (четырехмерное псевдоевклидово пространство – время). Частица описывает в четырехмерном пространстве кривую, которая называется мировой линией.
При плоском движении частицы в коор-динатной плоскости (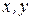 ) с постоянной скоростью
) с постоянной скоростью 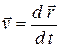 мировая линия частицы –прямая линия 1 (см. рисунок). Очевидно, что
мировая линия частицы –прямая линия 1 (см. рисунок). Очевидно, что  , где
, где 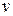 - скорость движения частицы. Мировая линия частицы, движущейся с ускорением – кривая 2.
- скорость движения частицы. Мировая линия частицы, движущейся с ускорением – кривая 2.
Траектории частиц всегда расположены внутри конуса, называемого световым конусом. Образующие этого конуса отвечают движению фотона, скорость которого равна  .
.
Рассмотрим элемент мировой линии частицы
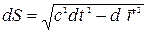 =
=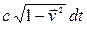 ,
, 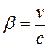 . (10.1)
. (10.1)
Введем собственное время частицы 
 . Очевидно, оно является инвариантом. Тогда
. Очевидно, оно является инвариантом. Тогда
 . (10.2)
. (10.2)
Обобщим понятие скорости в трех
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 2917; Нарушение авторских прав?; Мы поможем в написании вашей работы!