Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном СКО

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение неизвестно. Требуется оце­нить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно вос­пользоваться результатами предыдущего параграфа, в ко­тором а предполагалось известным.

Оказывается, чтопо данным выборки можно построить случайную величину(ее возможные значения будем обозначать через t ):

(4.12)

которая имеет распределение Стьюдента с k = n - 1 сте­пенями свободы; здесь 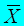- выборочная средняя, S - «исправленное» среднее квадратическое отклонение, n — объем выборки.

Плотность распределения Стьюдента

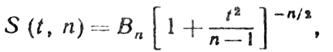(4.13)

где

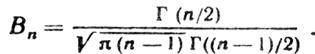(4.14)

Из выражений (4.13) и (4.14) видно, чтораспределение Стьюдента определяется параметром n - объемом выборки (или, что то же, чис­лом степеней свободы k = n - 1 )и не зависит от неиз­вестных параметров а и 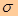. Эта особенность является его большим достоинством.Поскольку S(t, п) —четная функ­ция от t ,вероятность осуществления неравенства

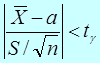(4.15)

определяется так:

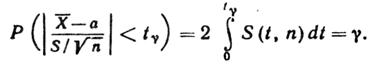(4.16)

Заменив неравенство в круглых скобкахравносильным ему двойным неравенством, получим

(4.17)

Итак, пользуясь распределением Стьюдента, найден доверительный интервал , по­крывающий неизвестный параметр а с надежностью .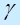

Здесь случайные величины и 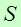заменены неслучайными величинами и 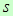, найденными по выборке. По специальной таблице и по заданным n и 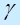можно найти .

4.4 Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое откло­нение по «исправленному» выборочному среднему квадратическому отклонению 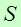. Поставим перед собой задачу найти доверительные интервалы, покрывающие параметр с заданной надежностью .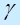

Потребуем, чтобы выполнялось соотношение:

(4.18)

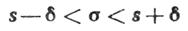Для того чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство

(4.13)

в равносильное неравенство

(4.14)

Положив 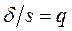, получим

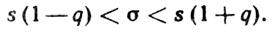(4.15)

Остается найти q. С этой целью введем в рассмотрение случайную величину «хи»:

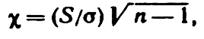
где n - объем выборки.

Можно доказать, чтовеличина 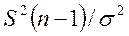распределена по закону с n - 1 степенями свободы, поэтомуквадратный корень из нее обозначают через

Плотность распределения имеет вид:

(4.16)

Это распределение не зависит от оцениваемого параметра , а зависит лишь от объема выборки п.

Преобразуем неравенство (4.15) так, чтобы оно приняло вид 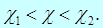Вероятность этого неравенстваравна заданной вероятности 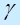, т. е.

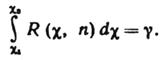(4.17)

Предполагая, что q < 1,перепишем неравенство (4.15) так:

(4.18)

Умножив все члены неравенства на , получим

(4.19)

или

(4.20)

Вероятность того, чтоэто неравенство, а следовательно, и равносильное ему неравенство (4.15) будет осуществлено, равна

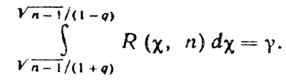(4.21)

Из этого уравнения можно, по заданным п и 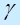, найти q. Практически для отыскания q пользуются специальной таблицей(см.приложения 3 метод.разр-ки практического зан.3.4).

Вычислив по выборке 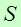и найдя по специальной таблице q, полу­чим искомый доверительный интервал (4.15), покрывающий с заданной надежностью 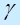, т. е. интервал

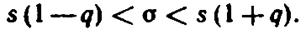Автор: К.Т.Н., доцент Куприянов В.Е.

5.11.12г

Дата добавления: 2014-01-05