Предел и непрерывность функции

ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ 8

ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ 3

Дополнительная

Основная

1. Пучков Л.А.. Жежелевский Ю.А. Подземная разработка месторождений полезных ископаемых. Учебник. М. 2007.

2. Егоров П.В., Бобер Е. А. и др. Основы горного дела. Учебник. 2-е изд. 2006.

3. Васильев А.В., Зубов В.П., Сиренко Ю.Г. Моделирование на ЭВМ стоимостных показателей горных работ в шахтах. Методические указания к расчетно-графическим работам для студентов горно-геологических специальностей. РИЦ Национального минерально-сырьевого университета " Горный " С. 75. 2012 г.

1. Килячков А.П. Технология горного производства. М., Недра, 1992.

2. Черняк И.Л., Ярунин С.А., Бурчаков Ю.И. Технология и механизация подземной добычи угля. М., Недра, 1981.

3. Бурчаков А.С., Гринько Н.К., Черняк И.Л. Процессы подземных горных работ. М., Недра, 1982

4. Задачник по подземной разработке угольных месторождений. Авт. Сапицкий К.Ф., Дорохов Д.В., Зборщик М.П., Андрушко В.Ф. М., Недра, 1981.

5. Васильев А.В., Сиренко Ю.Г. Моделирование на ЭВМ основных параметров шахты. / Санкт-Петербургский горный институт, СПБ, 1995.

ЭКСТРЕМУМ ФУНКЦИИ 14

Функции многих переменных – естественное обобщение функций одной переменной. Мы рассмотрим основы дифференциального исчисления функций двух переменных. Почему двух, а не трех или большего числа переменных? Во-первых, принципиального различия между двумя и большим числом переменных нет, увеличение числа переменных ведет лишь к громоздкости выкладок. Во-вторых, случай двух переменных допускает наглядную геометрическую интерпретацию.

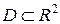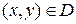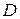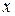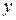1. Вводные понятия. Пусть дано множество , и пусть указано правило, по которому каждой точке соответствует некоторое число . В этом случае говорят, что задана функция с областью определения и областью значений . При этом и называют независимыми переменными (аргументами), а – зависимой переменной (функцией).

Функцию часто записывают в виде «». Схематично функция может быть изображена так, как это показано на рис. 1.

Рис.1.

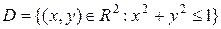Пример. На множестве определим функцию 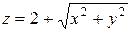; тогда ее областью значений является отрезок . Эту функцию можно определить, конечно, и на всей плоскости 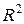; в этом случае имеем и .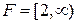

Графиком функции называют множество точек ; обычно графиком является некоторая поверхность (рис. 2).

При построении графика функции часто пользуются методом сечений.

Пример. Построить график функции 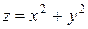и найти 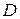. Рис.2.

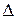Воспользуемся методом сечений.

– в плоскости – парабола.

– в плоскости –парабола.

– в плоскости – окружность.

Искомая поверхность – параболоид вращения (рис. 3). ▲ Рис.3.

Расстоянием между двумя произвольными точками и (евклидова) пространства 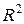называется число

.

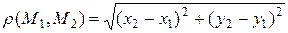Множество точек называется открытым кругом радиуса 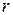с центром в точке 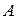, – окружностью радиуса 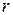с центром в точке .

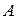Открытый круг радиуса 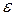с центром в точке 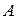называется 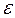-окрестностью точки .

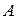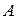Определение. Точка называется внутренней точкой множества 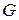, если существует 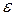-окрестность точки 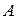, целиком принадлежащая множеству 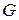(т.е. ) (рис. 4).

Определение. Точка 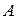называется граничной точкой множества 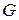, если в любой ее 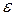-окрестности содержатся точки, как принадлежащие множеству 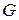, так и не принадлежащие ему (рис. 5). Рис.4.

Граничная точка множества может как принадлежать этому множеству, так и не принадлежать ему.

Определение. Множество 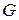называется откры-тым, если все его точки – внутренние.

Определение. Множество 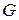называется замк-нутым, если оно содержит все свои граничные точки. Множество всех граничных точек множества 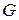называется его границей (и часто обозначается символом ). Заметим, что множество является замкнутым и называется замыканием множества 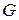. Рис.5.

Пример. Если , то . При этом . Покажите это!

Определение. Точка 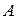называется предельной точкой множества 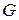, если в любой 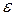-окрестности точки 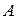содержатся точки множества 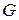, отличные от .

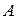Образно говоря, точка 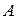называется предельной точкой множества 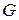, если «к точке 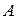можно подойти сколь угодно близко, идя по точкам множества 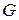и не наступая на саму точку 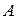». Предельная точка множества может принадлежать, а может не принадлежать этому множеству.

Пример. Множество совпадает с множеством своих предельных точек. Множество имеет единственную предельную точку . Покажите это!

Дата добавления: 2014-01-05