
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эффект Холла в полупроводниках
|
|
|
|
39.1. Определение
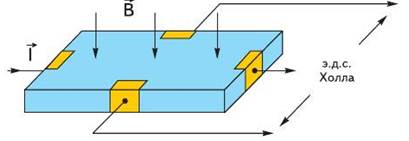 Эффект Холла – возникновение в твердом, помещенном в магнитное поле металле или полупроводнике электрического поля, перпендикулярного направлениям тока и магнитной индукции. Это поле называется полем Холла.
Эффект Холла – возникновение в твердом, помещенном в магнитное поле металле или полупроводнике электрического поля, перпендикулярного направлениям тока и магнитной индукции. Это поле называется полем Холла.
 39.2. Эффект Холла в металлах и полупроводниках
39.2. Эффект Холла в металлах и полупроводниках 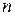 - или
- или 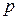 -типа
-типа
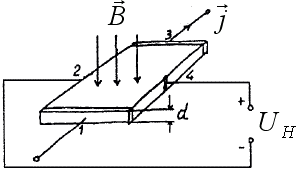
Для классического объяснения эффекта Холла рассмотрим однородную металлическую или полупроводниковую плоскопараллельную пластинку длиной 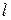 (между точками 1 и 3, рис. для электронной проводимости), высотой (толщиной)
(между точками 1 и 3, рис. для электронной проводимости), высотой (толщиной) 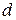 и шириной
и шириной 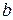 (между точками 2 и 4). Пусть
(между точками 2 и 4). Пусть 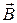 – магнитная индукция;
– магнитная индукция;  – плотность тока в образце. Для металла и полупроводников
– плотность тока в образце. Для металла и полупроводников 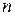 - или
- или 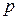 -типа плотность тока соответственно равна:
-типа плотность тока соответственно равна:
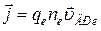 ,
, 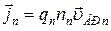 ,
, 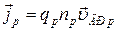 . (1)
. (1)
На движущийся в магнитном поле электрический заряд действует сила Лоренца 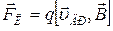 , под действием которой возникает поперечный ток: электроны и дырки будут отклоняться вправо, поэтому правая грань пластинки приобретет отрицательный или положительный заряд, а левая – зарядится противоположно. Заряженные грани создают поперечное электрическое поле между точками 2 и 4. Грани заряжаются до тех пор, пока не наступит равновесие, при котором силу Лоренца, действующую на носитель заряда, компенсирует противоположно направленная электрическая сила
, под действием которой возникает поперечный ток: электроны и дырки будут отклоняться вправо, поэтому правая грань пластинки приобретет отрицательный или положительный заряд, а левая – зарядится противоположно. Заряженные грани создают поперечное электрическое поле между точками 2 и 4. Грани заряжаются до тех пор, пока не наступит равновесие, при котором силу Лоренца, действующую на носитель заряда, компенсирует противоположно направленная электрическая сила 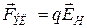 , и поперечный ток исчезает. Силы уравновешивают друг друга:
, и поперечный ток исчезает. Силы уравновешивают друг друга: 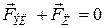 , следовательно,
, следовательно, 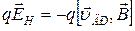 . Отсюда, согласно (1),
. Отсюда, согласно (1), 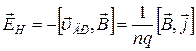 .
.
39.3. Константа Холла
Таким образом, напряженность поля Холла может быть вычислена по формуле:
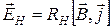 , (1)
, (1)
в которой коэффициент 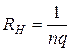 характеризует образец и эффект и называется постоянной Холла (более точная квантовая теория, учитывающая участие в токе электронов, обладающих различными скоростями, приводит к выражению
характеризует образец и эффект и называется постоянной Холла (более точная квантовая теория, учитывающая участие в токе электронов, обладающих различными скоростями, приводит к выражению 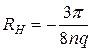 для постоянной Холла). Знак
для постоянной Холла). Знак 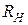 зависит от знака основных носителей заряда: если их заряд
зависит от знака основных носителей заряда: если их заряд 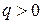 , то
, то 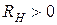 ; если
; если 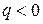 , то
, то 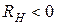 . Для каждого полупроводникового образца, находящегося при фиксированной температуре,
. Для каждого полупроводникового образца, находящегося при фиксированной температуре, 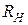 постоянна. Таким образом, при изучении эффекта Холла в металлах и полупроводниках
постоянна. Таким образом, при изучении эффекта Холла в металлах и полупроводниках 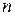 - или
- или 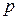 -типа, измерив
-типа, измерив 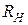 , можно найти концентрацию носителей
, можно найти концентрацию носителей 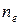 ,
, 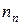 ,
, 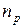 , а по знаку возникающей разности потенциалов Холла (рис.) – механизм проводимости полупроводников: для дырочного полупроводника
, а по знаку возникающей разности потенциалов Холла (рис.) – механизм проводимости полупроводников: для дырочного полупроводника 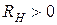 , а для электронного –
, а для электронного – 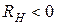 .
.
|
|
|
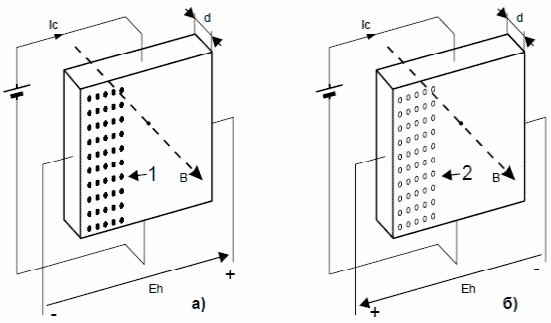
Рис. Полярность ЭДС Холла и поле Холла 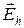 в полупроводнике а)
в полупроводнике а) 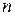 -типа; б)
-типа; б) 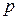 -типа.
-типа.
39.4. Разность потенциалов (ЭДС) Холла в металлах и полупроводниках 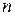 - или
- или 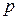 -типа
-типа
Пусть ток силой 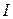 (рис.) течет от нас в направлении от точки 1 к точке 3, Индукция магнитного поля направлена вниз перпендикулярно верхней грани пластинки и перпендикулярно току. Сила и плотность тока связаны соотношением:
(рис.) течет от нас в направлении от точки 1 к точке 3, Индукция магнитного поля направлена вниз перпендикулярно верхней грани пластинки и перпендикулярно току. Сила и плотность тока связаны соотношением:
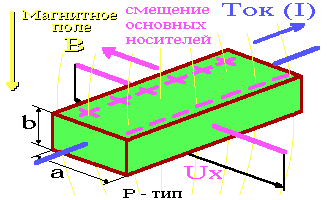
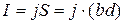 , (2)
, (2)
где 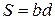 – площадь сечения, поперечного току. Между точками граней в направлении
– площадь сечения, поперечного току. Между точками граней в направлении 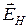 (точками 4 и 2 на рис. к п. 39.2) устанавливается разность потенциалов
(точками 4 и 2 на рис. к п. 39.2) устанавливается разность потенциалов
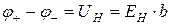 , (3)
, (3)
которая называется разностью потенциалов или ЭДС Холла. Если 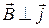 , то модуль
, то модуль 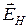 максимален и равен
максимален и равен  . Подставляя эту формулу в выражение (3) и учитывая (2), получим:
. Подставляя эту формулу в выражение (3) и учитывая (2), получим: 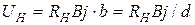 .
.
39.5. Эффект Холла в полупроводниках со смешанной или собственной проводимостью
Если полупроводник имеет смешанную или собственную проводимость, то проходящий в полупроводниковой пластинке ток обусловлен движением дырок и электронов в противоположных направлениях. Следовательно, направления отклонения дырок и электронов под действием магнитного поля совпадают: и те, и другие отклоняются одной грани пластинки. Возникающая разность потенциалов Холла, величина и знак 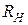 в этом случае будут зависеть от соотношения концентраций и подвижностей дырок и электронов и могут быть равны нулю.
в этом случае будут зависеть от соотношения концентраций и подвижностей дырок и электронов и могут быть равны нулю.
Найдем упрощенным способом постоянную Холла для общего случая. Для этого учтем, что на самом деле удельная проводимость – это тензор (матрица) коэффициентов 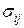 , определяемый законом Ома в дифференциальной форме
, определяемый законом Ома в дифференциальной форме 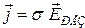 :
:
|
|
|
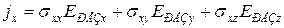 ;
;
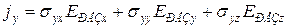 ; (1)
; (1)
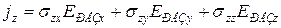 .
.
Пусть для простоты 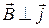 , то есть
, то есть 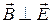 , где
, где 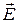 – напряженность электрического поля, вызывающего ток. Тогда
– напряженность электрического поля, вызывающего ток. Тогда 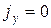 . Напряженность результирующего электрического поля вычисляется по принципу суперпозиции:
. Напряженность результирующего электрического поля вычисляется по принципу суперпозиции: 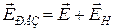 . Пусть
. Пусть 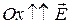 ,
, 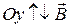 , следовательно,
, следовательно, 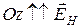 . Тогда проекции
. Тогда проекции 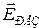 на оси равны:
на оси равны: 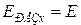 ;
; 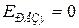 ,
, 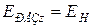 . Подставив значения проекций в систему уравнений (1), с учетом того, что в установившемся состоянии поперечного тока нет (
. Подставив значения проекций в систему уравнений (1), с учетом того, что в установившемся состоянии поперечного тока нет (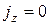 ) получим:
) получим:
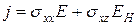 ;
;
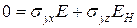 ; (2)
; (2)
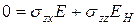 .
.
Так как от названия осей физика не зависит, уравнения симметричны относительно замены 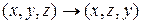 . Следовательно,
. Следовательно, 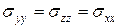 ;
; 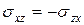 . Чтобы связать
. Чтобы связать 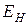 с
с 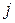 , выразим
, выразим 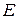 из третьего уравнения системы (2):
из третьего уравнения системы (2):
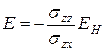 (3)
(3)
и подставим полученное выражение в первое уравнение: 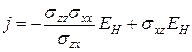 . Тогда
. Тогда 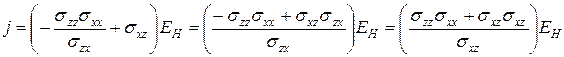 . Отсюда
. Отсюда
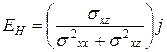 . (4)
. (4)
Для слабых магнитных полей 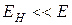 , следовательно, согласно (3),
, следовательно, согласно (3), 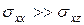 , поэтому,
, поэтому, 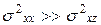 , и приближенно можно считать, что
, и приближенно можно считать, что 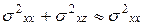 . Тогда формула (4) принимает вид:
. Тогда формула (4) принимает вид:
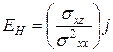 . (5)
. (5)
Плотность тока, текущего через полупроводниковую пластинку,  . При этом
. При этом  не сонаправлен с
не сонаправлен с 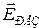 ! Проводимость
! Проводимость
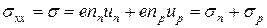 , (6)
, (6)
где 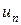 и
и 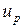 – подвижность носителей заряда в направлении
– подвижность носителей заряда в направлении 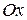 .
.
Чтобы найти 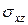 будем считать, что на каждый тип носителя заряда действует поле
будем считать, что на каждый тип носителя заряда действует поле 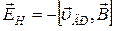 . Отсюда
. Отсюда
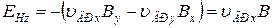 . (7)
. (7)
Из формулы (3) с учетом равенств 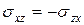 и (6):
и (6):
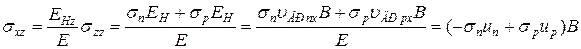 . (8)
. (8)
Подставив (8) в (5), получим:
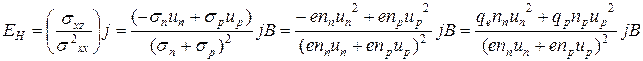 .
.
Таким образом, константа Холла 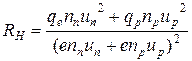 , с учетом квантово-статистических эффектов
, с учетом квантово-статистических эффектов 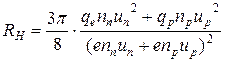 .
.
В случае собственной проводимости 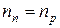 , поэтому
, поэтому 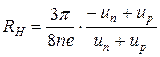 .
.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 20066; Нарушение авторских прав?; Мы поможем в написании вашей работы!