Реактор идеального смешения периодического действия

Гидродинамические модели реакторов. Вывод характеристических уравнений.

Лекция № 9

Ранее мы рассмотрели основные модели химических процессов и их математическое описание. Усложним модель химико-технологического процесса за счет учета гидродинамических процессов, то есть способов направленного движения потоков реакционной смеси в реакторе.

Любой реактор, используемый в химическом производстве. В большем или меньшем приближении можно описать одной из следующих моделей:

- реактор идеального смешения периодического действия РИС-П;

- реактор идеального смешения непрерывного действия РИС-Н;

- реактор идеального вытеснения непрерывного действия РИВ-Н;

- каскад реакторов идеального смешения непрерывного действия К-РИВ-Н (ячеечная модель).

Для каждой модели выведено характеристическое уравнение, которое выражает зависимость времени пребывания реагентов в реакторе о, начальной концентрации реагента, величины конверсии и скорости химической реакции.

τ = f (C_A0, α_A, r_A)

Это уравнение является математическим описанием модели реактора. Оно дает возможность, задав С_А0 (состав исходной смеси) и r_A (тип химической реакции, температуру, давление, катализатор и т.п.) рассчитать время пребывания реагентов в реакторе, необходимое для достижения заданной конверсии (α_A), а значит, и объем реактора, его габаритные размеры и производительность. Сравнивая полученные значения для реакторов разного типа, можно выбрать самый оптимальный вариант для проведения данной химической реакции.

Основанием для вывода характеристического уравнения является материальный баланс реактора, составленный по одному их компонентов реакционной смеси.

РИС-П представляет собой аппарат с мешалкой, в который периодически загружают исходные реагенты и также периодически выгружают продукты.

В таком реакторе создается такое интенсивное перемешивание, что в каждый момент времени концентрация реагентов одинакова по всему объему реактора и изменяется лишь во времени, по мере протекания химической реакции.

Исходным уравнением для получения характеристического уравнения является уравнение материального баланса в дифференциальной форме:

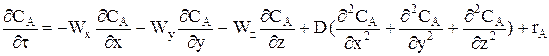
Так как вследствие интенсивного перемешивания все параметры одинаковы по всему объему реактора, в любой момент времени производная любого порядка от концентрации по осям x,y,z равна нулю.

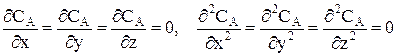
Тогда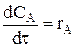

При V_{реакци.смеси} = const C_A = C_A0 (1-α_А).

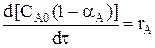
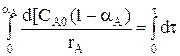
- характеристическое уравнение РИС-П

Если в реакторе протекает простая необратимая реакция «n»-го порядка, то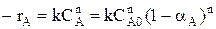

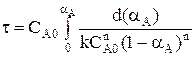
При n = 0 ,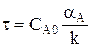

n = 1 .

При n ≠ 0 и 1 определение τ производят методом графического интегрирования. Для этого строят графическую зависимость

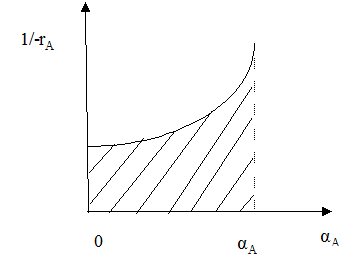
вычисляют площадь под кривой между начальным и конечным значением степени превращения.

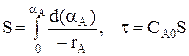
Дата добавления: 2014-01-05