
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П. 2. Предел функции многих переменных. Двойной и повторный пределы. Непрерывность функции многих переменных
|
|
|
|
Определение 1 (предела функции на языке 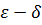 ).
).
Пусть точка  - точка сгущения множества
- точка сгущения множества  (не обязательно
(не обязательно  !). Пусть
!). Пусть 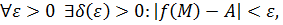 лишь только
лишь только  . Тогда говорят, что в точке
. Тогда говорят, что в точке  существует предел
существует предел 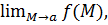 и он равен
и он равен  :
:
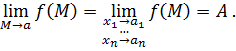
Определение 2. Говорят, что последовательность точек  сходится к числу
сходится к числу  при
при 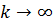 (обозначим
(обозначим  ), если
), если  при
при 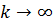 .
.
Очевидно, можно записать и так:
 при
при 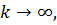 если
если  .
.
Определение 3 (предела на языке последовательностей).
Пусть точка  - точка сгущения множества
- точка сгущения множества  (не обязательно
(не обязательно  !). Пусть
!). Пусть  выполнено
выполнено  . Тогда говорят, что
. Тогда говорят, что 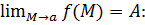

Можно доказать, что два определения предела (определения 1 и 3) эквивалентны.
Выше рассмотрен предел функции  при одновременном стремлении независимых переменных
при одновременном стремлении независимых переменных 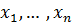 к их пределам. Такой предел называется
к их пределам. Такой предел называется  - кратным (или двойным, тройным и т.д. при
- кратным (или двойным, тройным и т.д. при 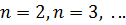 ).
).
Можно рассматривать и пределы, получаемые в результате нескольких последовательных переходов по каждой переменной в отдельности, в том или ином порядке. Такие пределы называются повторными.
Пример. Рассмотрим повторные пределы функции 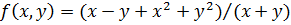 при
при 
Имеем:
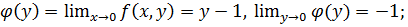

Видим, что
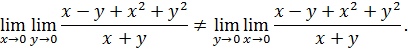
Пусть функция 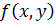 определена в области
определена в области 
 ). Пусть для любого фиксированного
). Пусть для любого фиксированного  из
из  существует предел
существует предел

и для любого фиксированного 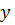 из
из 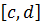 существует предел
существует предел

Рассмотрим пределы
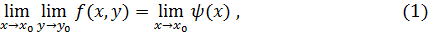


Справедлива следующая теорема.
Теорема (о повторных пределах, без доказательства). Пусть
1. Функция  определена в области
определена в области 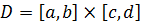 ,
,  ,
,
2. Существует (конечный или нет) двойной предел (3):
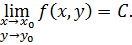
3. 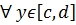 существует конечный простой предел по
существует конечный простой предел по 
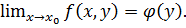
Тогда существует повторный предел (2) 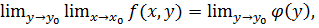
и он равен двойному (= C).
Следствия.
1. Если, кроме 1. и 2., существует конечный предел по 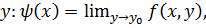 то существует и второй повторный предел
то существует и второй повторный предел
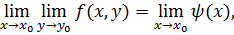
и он тоже равен C.
2. Если повторные пределы (1), (2) существуют, конечны, но не равны между собой, то двойной предел (3) не существует.
|
|
|
Замечание. Может оказаться, что двойной предел существует, а повторный – нет. Например,

но повторный предел  не существует.
не существует.
Определение 4. Функция  называется бесконечно малой при
называется бесконечно малой при  если
если 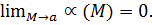
Определение 5. Бесконечно малая  называется бесконечно малой более высокого порядка малости при
называется бесконечно малой более высокого порядка малости при  чем бесконечно малая
чем бесконечно малая  если
если
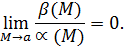
Пусть множество 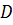 является областью определения функции
является областью определения функции 
 – внутренняя точка множества
– внутренняя точка множества 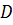 .
.
Определение 6. Функция 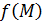 называется непрерывной в точке
называется непрерывной в точке  , если
, если
1) существует 
2) 
Определение 7 (непрерывности на языке  ).
).
Функция 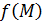 называется непрерывной в точке
называется непрерывной в точке  , если
, если
 лишь только
лишь только  .
.
Определение 8 (непрерывности на языке последовательностей).
Функция 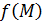 называется непрерывной в точке
называется непрерывной в точке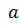 , если
, если
 выполнено
выполнено 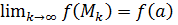 .
.
Определение 9 (непрерывности на языке приращений).
Пусть  - приращение функции
- приращение функции 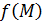 :
: Пусть выполнено
Пусть выполнено

Тогда функция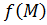 называется непрерывной в точке
называется непрерывной в точке 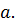
Замечание. Рассмотрим функцию  . Фиксируем все переменные, кроме одной, например, переменной
. Фиксируем все переменные, кроме одной, например, переменной  :
: 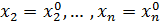 . Получим функцию одной переменной
. Получим функцию одной переменной  :
: 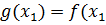 ,
, 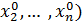 .). Если окажется, что построенная функция
.). Если окажется, что построенная функция 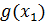 в точке
в точке 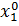 непрерывна, то говорят, что функция
непрерывна, то говорят, что функция  непрерывна по переменной
непрерывна по переменной  в точке (
в точке (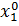 ,
, 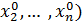 .
.
Очевидно, что, если функция  непрерывна по совокупности переменных в точке (
непрерывна по совокупности переменных в точке ( ), то она непрерывна по каждой переменной в отдельности в этой точке.
), то она непрерывна по каждой переменной в отдельности в этой точке.
Обратное, вообще говоря, неверно. Может оказаться, что функция  непрерывна в точке
непрерывна в точке 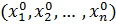 по каждой переменной в отдельности, но не является непрерывной по совокупности переменных.
по каждой переменной в отдельности, но не является непрерывной по совокупности переменных.
Пример. Рассмотрим функцию 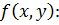

Здесь 
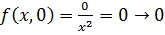 при
при 
 при
при 
Следовательно, функция 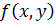 является непрерывной по каждой переменной в отдельности в точке
является непрерывной по каждой переменной в отдельности в точке 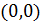 , но она не является непрерывной по совокупности переменных в этой точке, так как двойной предел функции
, но она не является непрерывной по совокупности переменных в этой точке, так как двойной предел функции 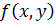 в этой точке не существует.
в этой точке не существует.
Определение 10. Функция  называется равномерно непрерывной на множестве
называется равномерно непрерывной на множестве 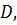
|
|
|
если 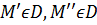 таких, что
таких, что 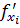 :
:
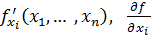 .
.
Запишем определение частных производных для случая двух переменных x, y:
 .
.
Замечания.
1. Из существования частных производных в точке, вообще говоря, не следует непрерывность функции в данной точке. Рассмотрим, например, функцию
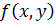 :
:

Эта функция обладает частными производными по переменным x, y в точке 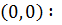
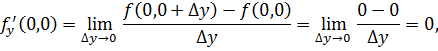
но, тем не менее, не является непрерывной в этой точке (докажите это!).
2. Из непрерывности функции в точке, вообще говоря, не следует существование частных производных в этой точке. Например, функция  является непрерывной в точке
является непрерывной в точке 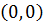 , но частные производные этой функции не существуют в точке
, но частные производные этой функции не существуют в точке 
3. Частная производная функции 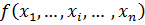 по переменной
по переменной 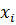 в точке
в точке 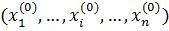 является обычной производной функции одной переменной
является обычной производной функции одной переменной 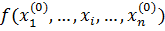 по переменной
по переменной 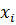
 Рассмотрим геометрический смысл частной производной. Рассмотрим случай функции двух переменных:
Рассмотрим геометрический смысл частной производной. Рассмотрим случай функции двух переменных: 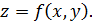 Это уравнение описывает в трехмерном пространстве поверхность
Это уравнение описывает в трехмерном пространстве поверхность  . Пусть точка
. Пусть точка  (
( принадлежит области определения функции
принадлежит области определения функции 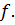 Построим плоскость
Построим плоскость 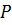 , проходящую через точку (
, проходящую через точку (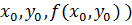 параллельно плоскости
параллельно плоскости  . Обозначим линию пересечения плоскости
. Обозначим линию пересечения плоскости 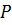 и поверхности
и поверхности  символом
символом 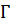 :
: 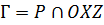 . Построим прямую
. Построим прямую 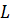 - касательную к кривой
- касательную к кривой 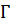 . Обозначим через
. Обозначим через  угол между прямой
угол между прямой 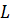 и плоскостью
и плоскостью  Тогда
Тогда
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 4277; Нарушение авторских прав?; Мы поможем в написании вашей работы!