Независимость

Понятие независимости является ключевым в теории вероятностей и поэтому очень важно правильно его понимать. Без ясного понимания этого понятия, все дальнейшие положения теории вероятностей будут трактоваться неправильно.

Определение События A и B называются независимыми, если P(A×B) = P(A)×P(B).

Отсюда следует, что: P(A | B) = P(A × B)/P(B) = [P(A)×P(B)]/P(B) = P(A), (P(B) ≠ 0)

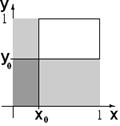Пример 6 Точка с координатами (x; y) бросается наудачу в единичный квадрат W со сторонами, параллельными осям координат. Доказать, что для любой заранее выбранной точки единичного квадрата с координатами (x ₀; y ₀) Î W события: A = { x ≤ x ₀} и B = { y ≤ y ₀} являются независимыми.

| W | = 1×1 = 1, | A | = x ₀×1 = x ₀, P(A) = | A | / | W | = x ₀.

| B | = y ₀×1 = y ₀, P(B) = | B | / | W | = y ₀.

P(A × B) = | A × B | / | W | = x ₀× y ₀, но P(A)×P(B) = x ₀× y ₀ → события A и B независимы.

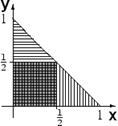Пример 7 Точка с координатами (x; y) бросается наудачу в треугольник с вершинами (1; 0), (0; 0), (0; 1). Доказать, что события A = { x ≤ 1/2} и B = { y ≤ 1/2} зависимы.

| W | = (1×1)/2 = 1/2, | A | = ¼ + 1/8 =3/8, P(A) = | A | / | W | = 3/4.

| B | = ¼ + 1/8 = 3/8, P(B) = | B | / | W | = 3/4.

P(A × B) = | A × B | / | W | = (1/4) / (1/2) = ½, но P(A)×P(B) = 9/16 → события A и B зависимы.

Замечание 1 Несовместные события A и B будут независимыми только в вырожденном случае, когда P(A) = 0 или P(B) = 0.

В невырожденном случае, когда P(A) ≠ 0 и P(B) ≠ 0 несовместные события не могут быть независимыми. Зависимость между ними следует из простой причинно-следственной связи: т.к. A Ì 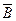, то при наступлении события A обязательно наступает событие 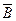, т.е. событие B обязательно не наступает, а это уже зависимость!

Это же можно сформулировать иначе: в невырожденном случае независимые события просто обязаны пересекаться, т.е. обязаны быть совместными.

Замечание 2 Если события A и B независимы, то независимыми являются также события: A и 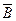, B и Ẵ, Ẵ и 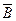(без доказательства).

Замечание 3 По аналогии с определением независимости двух событий A и B может показаться, что при бóльшем числе событий A ₁, A ₂, …, A _n достаточно выполнение одного только равенства P(A ₁× A ₂×…× A _n) = P(A ₁)×P(A ₂)×…×P(A _n), чтобы считать эти события независимыми. Однако из этого равенства вовсе не следует, что, например, события A ₁ и A ₂ являются независимыми. Независимостью нескольких событий следует считать такое их свойство, при котором любые мыслимые комбинации произведений этих событий являются независимыми между собой.

Определение События А₁, А₂, …, А _n называются независимыми в совокупности, если для любого 1 ≤ k ≤ n и любого набора различных между собой индексов 1 ≤ i₁, i₂…i_k ≤ n выполняется равенство: P(A _i1× A _i2×…× A _ik) = P(A _i1)×P(A _i2)×…×P(A _ik).

Замечание 4 Если события А ₁, А ₂… А _n независимы в совокупности, то они попарно независимы, т.е. любые два события А _i, А _j независимы, но обратное утверждение неверно.

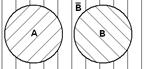
Пример 8 (С.Н.Бернштейн) Рассмотрим правильный тетраэдр, 3 грани которого окрашены, соответственно, в красный, синий и зеленый цвета, а четвертая грань окрашена во все три этих цвета. Пусть событие A означает, что при бросании тетраэдра он упал на грань, содержащую красный цвет, событие B – синий цвет и событие C – зеленый цвет.

Вероятность наступления каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырех. Вероятность одновременного наступления любых двух из них равна 1/4, так как только одна грань является многоцветной. А так как (1/2) (1/2) = 1/4, то все события являются попарно независимыми. Но вероятность одновременного наступления всех трех событий тоже равна 1/4, а не 1/8 как следовало бы для независимых событий, то есть события не являются независимыми в совокупности.

Дата добавления: 2014-01-05