Случайные величины и их распределения

Приближенная формула Пуассона для схемы Бернулли

Предположим, нас интересует вероятность получить три успеха в 1000 испытаний по схеме Бернулли с вероятностью единичного успеха 0,0001. Вероятность этого события равна:

P ₁₀₀₀(3) = C ³₁₀₀₀×0,0001³×0,9999⁹⁹⁷, но вычислить это выражение довольно сложно. Как быть?

Теорема Пуассона Пусть в испытаниях по схеме Бернулли n → ∞ и p → 0 так, что n×p → λ > 0. Тогда вероятность получить k успехов стремится к величине:

P_n(k) = C^k_n × p^k × q^n–k → λ^k×e^–λ / k! (11)

при этом абсолютная погрешность не превышает величины δ = n × p².

Таким образом, мы сами можем решать, достаточно ли n велико, а p мало, руководствуясь полученной величиной погрешности δ. На практике пуассоновским приближением пользуются, когда n × p × q ≤ 9.

Теперь мы можем вернуться к нашей задаче, в которой: n = 1000, p = 0,0001, λ = n × p = 1000×0,0001 = 0,1 и k = 3. Подставив значения этих параметров в формулу (14), получаем:

P ₁₀₀₀(3) = 0,1³× e ^–0,1 / 3! = 0,001×(2,718281828)^–0,1 / 6 ≈ 0,000151; (δ = 0,000001).

Если n × p × q ≥ 9, то для расчетов используют приближение Муавра-Лапласа.

Локальная теорема Муавра-Лапласа Пусть в испытаниях по схеме Бернулли n → ∞ и p → 0 так, что n×p → λ > 0. Тогда вероятность получить k успехов стремится к величине:

P_n(k) = C^k_n × p^k × q^n–k → exp(–x²/2) / (2π n×p×q)^1/2 (12)

при этом величина x = (k – n×p) / (n×p×q)^1/2 должна быть ограниченной при n → ∞.

Теорема Бернулли Если k – число успехов в n испытаниях Бернулли с вероятностью p успеха в одном испытании, то для любого ε > 0 справедливо соотношение:

lim_{n → ∞} P(|k/n – p| < ε) = 1 или, что то же самое lim_{n → ∞} P(k/n) = p.

Это означает, что с ростом числа испытаний n относительная частота успехов k/n приближается к значению вероятности p – успеха в одном испытании.

Переход от понятия случайного события к понятию случайной величины – это обобщение ранее полученных результатов на более высоком уровне абстракции, т.е. переход от словесных описаний частных случаев к математическим описаниям общих закономерностей, из которых эти частные случаи вытекают.

Случайные величины и их функций распределения является основными объектами изучения теории вероятностей.

Определение Пусть имеется пространство элементарных исходов Ω и на нем построено поле событий, причем для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному исходу g_i из Ω сопоставим число ξ_i. При этом потребуем, чтобы для любого х (–∞ < x <+∞) множество А тех g, для которых ξ < x, принадлежало полю событий, т.е. для него определена вероятность Р{ξ < x} = P(A) = F(x). Тогда ξ называется случайной величиной, а F(x) – ее функцией распределения.

Проще говоря, случайная величина – это величина, значение которой зависит от случая, если для всех х известна функция распределения F(x), т.е. вероятность того, что значение случайной величины меньше х.

Задание пространства элементарных исходов в определении случайной величины означает по существу задание условий, при которых возникают те или иные значения случайной величины, а если эти условия заданы, то тем самым определена и функция распределения F(x).

Например, нельзя просто сказать, что "температура – случайная величина". Но "температура воздуха, измеряемая на данной метеостанции в случайный момент времени в течение года" – это случайная величина, или "температура воздуха в случайно выбранной точке земного шара 1 января 2007 г. в 12.00 по московскому времени" – это другая случайная величина.

Свойства функции распределения:

1. F(–∞) = 0.

2. F(+∞) = 1.

3. F(x) – не убывающая функция.

Случайные величины могут быть непрерывными, т.е. принимать любые значения в некотором интервале (например, упомянутые выше температуры). Для них функция распределения F(x) – непрерывная функция.

Случайные величины могут быть дискретными, т.е. принимать конечное или счетное множество определенных значений (например, число очков при бросании игральной кости; число телефонных звонков, поступающих конкретному абоненту в течение суток). Для таких величин функция распределения F(x) имеет разрывы в точках, соответствующих принимаемым значениям случайной величины.

Дискретные величины удобнее характеризовать указанием возможных значений и соответствующих им вероятностей (вариационный ряд).

Пример 12 Число очков, выпадающих при бросании игральной кости.

хi	1	2	3	4	5	6
p(хi)	1/6	1/6	1/6	1/6	1/6	1/6

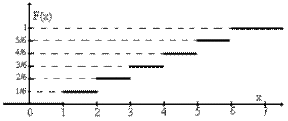Функция распределения:

Хотя случайная величина принимает только дискретные значения ее функция распределения определена для любых х.

Для непрерывных случайных величин вводится понятие плотности распределения f(х), которая представляет собой производную от функции распределения F(x):

f(х) = dF(x) / dx; F(x) = ∫^x_–∞ f(t)×dt.

Вероятность того, что случайная величина ξ примет значение, лежащее в интервале [а; b) равна разности значений функции распределения на концах интервала:

P(a≤ ξ <b) = F(b) – F(a).

Для непрерывных случайных величин можно кроме этого дополнительно записать:

P(a≤ ξ <b) = ∫^b_a f(t)×dt.

Важно помнить, что всегда: для дискретных распределений ∑p(х_i) = 1, а для непрерывных распределений ∫^+∞_–∞ f(t)×dt = 1.

Дата добавления: 2014-01-05