Методика изучения числовых равенств и неравенств

Числовое равенство – это запись, состоящая из двух числовых выражений, соединённых знаком равенства (5=5, 5+6=7+4, 4+5=10-1, (4:2+5)*3=21).

Числовое неравенство – это запись, состоящая из двух числовых выражений, соединённых знаками <, >(5<8, 5+6>4, 4<10-1, 4:2<21:7).

Числовые равенства и неравенства бывают верные (5+6=7+4, 4<10-1) и неверные (5+6=7-4, 4+6<10-1).

Сначала учитель вводит понятие верного числового равенства. Первое представление создаётся о них при сравнении чисел, которое основано на сравнении соответствующих множеств.

В 1 классе при изучении нумерации в концентре «Десяток» дети начинают сравнивать числа, устанавливая взаимно – однозначное соответствие между множествами. Учитель предлагает детям выложить перед собой 4 квадрата, а под ними 3 треугольника. 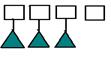Затем дети должны показать карточки с числами, которым соответствуют количества данных фигур. Сравните, каких фигур больше (больше квадратиков, т.к. у всех треугольников есть пара, а у одного квадрата нет пары). Делается вывод (квадратиков больше, чем треугольников, значит 4>3).

В дальнейшем, дети сравнивают числа, используя их расположение в натуральном ряду: 4>3, т. к. 4 называется позже при счёте.

В конце 1 класса при изучении нумерации в концентре «Сотня» добавляется новый приём сравнения чисел – поразрядное сравнение: 14 >13, т.к. 4ед. > 3ед.

Позже дети учатся сравнивать величины. Сначала величины, выраженные в одних единицах измерения: 5м >3м, а потом величины, выраженные в разных единицах измерения и связанные с разрядными единицами: 5дес. >40ед., т.к. 5дес.=50ед., а 50ед. >40ед., 5дм >40см., т.к. 5дм=50см, а 50см >40см.

При изучении нумерации в концентре «Тысяча» и «Многозначные числа» продолжают использовать поразрядное сравнение многозначных чисел: 4563<4653, т.к. 5ед. тыс. <6 ед. тыс., и величин, выраженных в разных единицах измерения

5м 32см<52дм 32см, т.к. 5м=50дм, 2дм=20см, а 32см<52см.

Позже рассматривается сравнение числовых выражений с числом. Сначала это сравнение происходит с опорой на соответствующие множества. Например, надо сравнить 3+1 и 3. Что больше?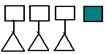Для этого учитель предлагает детям выложить перед собой 4 квадрата и под ними столько же треугольников. Сколько треугольников выложили? (3) А теперь придвиньте ещё один квадрат. Сколько стало квадратов? (4). Как узнали? (к 3 квадратам прибавили ещё 1). Каким выражением это можно записать? (3+1). Каких же фигур теперь больше? (квадратов). Что нам необходимо было сравнить? (3+1 и 3). Что мы для этого сделали? (узнали, сколько будет 3+1, и сравнили с 3). Значит, чтобы сравнить числовое выражение с числом, надо найти значение этого выражения и сравнить его с данным числом.

Затем дети учатся сравнивать два числовых выражения с использованием наглядности.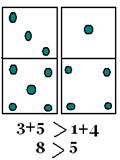Учитель организует наблюдение и помогает учащимся сделать вывод: для того чтобы сравнить два числовых выражения, надо выполнить указанные действия и сравнить получившиеся значения этих выражений.

В дальнейшем дети учатся сравнивать выражения, не вычисляя их значения, а пользуясь изученными свойствами и закономерностями. Например:

21*3<21*4+21, т. к. слева по 21 взяли 3 раза, а справа 5 раз (конкретный смысл умножения).

14-5<14-2, т.к. чем больше вычитаемое, тем меньше разность при одном и том же уменьшаемом, а 14=14 и 5>2.

(12+5)*8>12*8+5, т. к. при умножении суммы на число надо умножить число на каждое слагаемое, а здесь 5*8>5.

По программе Петерсон, не вычисляя, сравнивают буквенные неравенства 5а>3а, т.к. при одном постоянном множителе, чем больше другой множитель, тем больше произведение.

Непосредственно с понятием равенства и неравенства знакомят во 2 классе. Детям предлагается разбить на две группы записи и объяснить свой выбор:, 5+6=7+4, 4+5=10-1,,5<8, 5+6>4, 5=5, 4<10-1, 4:2<21:7,(4:2+5)*3=21. Дети формируют группы

5=5, 5+6=7+4, 4+5=10-1, (4:2+5)*3=21 и 5<8, 5+6>4, 4<10-1, 4:2<21:7. объясняя это тем, что в первой группе присутствует знак равенства, а во второй знаки неравенства. После этого учитель сообщает определения, и знакомит с понятием верного и неверного равенства и неравенства.

Для закрепления учитель предлагает:

§ Выбрать из перечисленных записей равенства, неравенства.

§ Выбрать из перечисленных равенств и неравенств верные, неверные, объяснить свой выбор.

§ Проверить, верны ли равенства.

Дата добавления: 2014-01-05