Метод прогноза и коррекции

Метод прогноза и коррекции относится к задачам класса Коши, а именно к численным решениям многошаговыми методами.

Рассмотрим задачу Коши:

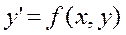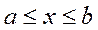, (2.1.1)

Подставим в (2.1.1) точное решение y(x), и проинтегрируем это уравнение на отрезке , тогда получим:

(2.1.2)

где в последнем член предполагаем, что p(x) полином, аппроксимирующий f(x,y(x)). Чтобы построить этот полином, предположим, что 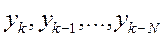- приближения к решению в точках . Будем считать для начала, что узлы Xi расположены равномерно с шагом h. тогда fi = f(xi,yi), (i=k,k-1,k-2,…,k-N) есть приближения к f (x,y(x)) в точках и мы в качестве P возьмем интерполяционный полином для выбора данных (xi,fi),

(i =k,k-1,k-2,…,k-N). Таким образом, P – полином степени N, удовлетворяющий условиям P(xi)=fi, (i = k,k-1,k-2,…,k-N). В принципе, можем проинтегрировать этот полином явно, что ведет к следующему методу:

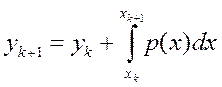(2.1.3)

В простейшем случае, когда N=0, полином P есть константа, равная fk, и (2.1.3) превращается в обычный метод Эйлера:

(2.1.4)

Если N=1, то P есть линейная функция, проходящая через точки

(xk-1,fk-1) и (xk,fk), т.е.

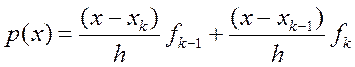(2.1.5)

интегрируя этот полином от Xk до Xk+1, получим следующий метод:

(2.1.6)

который является двухшаговым, поскольку использует информацию в двух точках xk и xk-1. Аналогично, если N=2, то P - есть кубический интерполяционный полином, а соответствующий метод определяется формулой:

(2.1.7)

Отметим, что метод (2.1.6) – есть метод Адамса-Башфорта второго порядка, (2.1.7) – метод Адамса-Башфорта четвертого порядка.

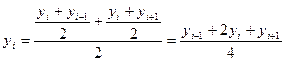
По 4 точкам:

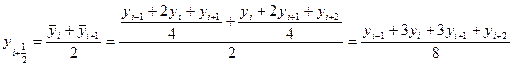
По 5 точкам:

Треугольник Паскаля 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 5 1

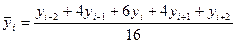
Для крайних точек:

По 3м точкам

По 5 точкам

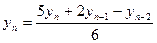
Для неравностоящих точек

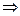
Если задана функция y(x), то это означает, что любому допустимому значению х сопоставлено значение у. Но нередко оказывается, что нахождение этого значения очень трудоёмко. Например, у(х) может быть определено как решение сложной задачи, в которой х играет роль параметра или у(х) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно. Функция у(х) может участвовать в каких-либо физико­-технических или чисто математических расчётах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у(х) приближённой формулой, то есть подобрать некоторую функцию j(х), которая близка в некотором смысле к у(х) и просто вычисляется. Затем при всех значениях аргумента полагают у(х)»j(х).

Большая часть классического численного анализа основывается на приближении многочленами, так как с ними легко работать. Однако для многих целей используются и другие классы функций.

Выбрав узловые точки и класс приближающих функций, мы должны ещё выбрать одну определённую функцию из этого класса посредством некоторого критерия — некоторой меры приближения или «согласия». Прежде чем начать вычисления, мы должны решить также, какую точность мы хотим иметь в ответе и какой критерий мы изберём для измерения этой точности.

Всё изложенное можно сформулировать в виде четырёх вопросов:

1. Какие узлы мы будем использовать?

2. Какой класс приближающих функций мы будем использовать?

3. Какой критерий согласия мы применим?

4. Какую точность мы хотим?

Существуют 3 класса или группы функций, широко применяемых в численном анализе. Первая группа включает в себя линейные комбинации функций 1, х, х², …, хⁿ, что совпадает с классом всех многочленов степени n (или меньше). Второй класс образуют функции cos a_ix, sin a_ix. Этот класс имеет отношение к рядам Фурье и интегралу Фурье. Третья группа образуется функциями e^-az. Эти функции встречаются в реальных ситуациях. К ним, например, приводят задачи накопления и распада.

Что касается критерия согласия, то классическим критерием согласия является «точное совпадение в узловых точках». Этот критерий имеет преимущество простоты теории и выполнения вычислений, но также неудобство из-за игнорирования шума (погрешности, возникающей при измерении или вычислении значений в узловых точках). Другой относительно хороший критерий — это «наименьшие квадраты». Он означает, что сумма квадратов отклонений в узловых точках должна быть наименьшей возможной или, другими словами, минимизирована. Этот критерий использует ошибочную информацию, чтобы получить некоторое сглаживание шума. Третий критерий связывается с именем Чебышева. Основная идея его состоит в том, чтобы уменьшить максимальное отклонение до минимума. Очевидно, возможны и другие критерии.

Более конкретно ответить на поставленные 4 вопроса можно лишь исходя из условий и цели каждой отдельной задачи.

Интерполяция многочленами

Цель задачи о приближении (интерполяции): данную функцию у(х) требуется приблизительно заменить некоторой функцией j(х), свойства которой нам известны так, чтобы отклонение в заданной области было наименьшим. интерполяционные формулы применяются, прежде всего, при замене графически заданной функции аналитической, а также для интерполяции в таблицах.

Методы интерполяции Лагранжа и Ньютона

Один из подходов к задаче интерполяции — метод Лагранжа. Основная идея этого метода состоит в том, чтобы прежде всего найти многочлен, который принимает значение 1 в одной узловой точке и 0 во всех других. Легко видеть, сто функция

является требуемым многочленом степени n; он равен 1, если x=x_j и 0, когда x=x_i, i¹j. Многочлен L_j(x)×y_j принимает значения y_i в i-й узловой точке и равен 0 во всех других узлах. Из этого следует, что есть многочлен степени n, проходящий через n+1 точку (x_i, y_i).

Другой подход — метод Ньютона (метод разделённых разностей). Этот метод позволяет получить аппроксимирующие значения функции без построения в явном виде аппроксимирующего полинома. В результате получаем формулу для полинома P_n, аппроксимирующую функцию f(x):

P(x)=P(x₀)+(x-x₀)P(x₀,x₁)+(x-x₀)(x-x₁)P(x₀,x₁,x₂)+…+

(x-x₀)(x-x₁)…(x-x_n)P(x₀,x₁,…,x_n);

— разделённая разность 1-го порядка;

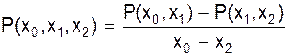— разделённая разность 2-го порядка и т.д.

Значения P_n(x) в узлах совпадают со значениями f(x)

Фактически формулы Лагранжа и Ньютона порождают один и тот же полином, разница только в алгоритме его построения.

Сплайн-аппроксимация

Другой метод аппроксимации — сплайн-аппроксимация — отличается от полиномиальной аппроксимации Лагранжем и Ньютоном. Сплайном называется функция, которая вместе с несколькими производными непрерывна на отрезке [a, b], а на каждом частном интервале этого отрезка [x_i, x_i+1] в отдельности являются некоторым многочленом невысокой степени. В настоящее время применяют кубический сплайн, то есть на каждом локальном интервале функция приближается к полиному 3-го порядка. Трудности такой аппроксимации связаны с низкой степенью полинома, поэтому сплайн плохо аппроксимируется с большой первой производной. Сплайновая интерполяция напоминает лагранжевую тем, что требует только значения в узлах, но не её производных.

Метод наименьших квадратов

Предположим, что требуется заменить некоторую величину и делается n измерений, результаты которых равны x_i=x+e_i (i=1, 2, …, n), где e_i — это ошибки (или шум) измерений, а х — истинное значение. Метод наименьших квадратов утверждает, что наилучшее приближённое значение есть такое число, для которого минимальна сумма квадратов отклонений от :

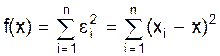
Один из наиболее общих случаев применения этого метода состоит в том, что имеющиеся n наблюдений (x_i, y_i) (i=1, 2, …, n) требуется приблизить многочленом степени m<n

y(x)=a₀+a₁x+a₂x²+…+a_mx^m

Вычисленная кривая у(х) в некотором смысле даёт сложное множество значений у_i. Метод наименьших квадратов утверждает, что следует выбирать многочлен, минимизирующий функцию.



Для нахождения минимума дифференцируем  по каждой из неизвестных a_k. В результате получим:

Определитель этой системы отличен от нуля и задача имеет единственное решение. Но система степеней не ортогональна, и при больших значениях n задача плохо обусловлена. Эту трудность можно обойти, используя многочлены ортогональные с заданным весом на заданной системе точек, но к этому прибегают только в задачах, связанных с особенно тщательной статической обработкой эксперимента.

Полиномы Чебышева

Критерии согласия данного метода — минимизация максимальной ошибки.

Полиномы Чебышева определяются следующим образом: T_n(x)=cos(n×arccos(x))

Например: T₀(x)=cos(0)=1,

T₁(x)=cos(q)=x,

T₂(x)=cos(2q)=cos²(q)-sin²(q)=2x²-1.

Можно было бы и дальше использовать тригонометрические соотношения для нахождения полиномов Чебышева любого порядка, но будет лучше установить для них рекурентное соотношение, связывающее T_n+1(x), T_n(x) и T_n-1(x):

T_n+1(x)=cos(nq+q)=cos(nq)cos(q)-sin(nq)sin(q),

T_n-1(x)=cos(nq-q)=cos(nq)cos(q)-sin(nq)sin(q).

Складывая эти неравенства, получим:

T_n+1(x)+T_n-1(x)=2cos(nq)cos(q)=2xT_n(x);

T_n+1(x)=2xT_n(x)-T_n-1(x).

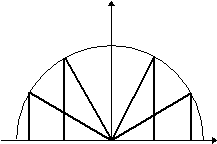
  Рис. 1

Применяя полученные формулы можно найти любой полином Чебышева. Например, Т₃(x)=2xT₂(x)-T₁(x). Подставляя значения T₂(х) и Т₁(х) имеем Т₃(х)=2х(2х²-1)-х=4х³-3х. Графически первые 10 полиномов Чебышева изображены ниже. Последующие полиномы по-прежнему колеблются между +1 и -1, причём период колебания уменьшаются с ростом порядка полинома.

Преобразования q=arccos(x) можно рассматривать как проекцию пересечения полукруга с множеством прямых, имеющих равные углы между собой (рис.1). Таким образом, множество точек x_j, на котором система чебышевских многочленов T_n(x) ортогональна, таково:

, (j=0, 1, 2, …,N-1)

Так как T_n(x) есть, по существу, cos(nq), то они являются равноколеблющимеся функциями, и так как они многочлены, то обладают всеми свойствами ортогональных многочленов.

Чебышев показал, что из всех многочленов Р_n(x) степени n старшим коэффициентом 1, у многочлена точная верхняя грань абсолютных значений на интервале -1£x£1 наименьшая. Так как верхняя грань T_n(x)=1, óêàçàííàÿ âåðõíÿÿ ãðàíü ðàâíà .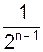

Дата добавления: 2014-01-05