Вычисление линейных рекуррентных последовательностей

Функции от матриц

Пусть f (t) некоторый многочлен, и требуется вычислить значение матрицы A от этого многочлена. В арифметическом пространстве матрица A задает линейное преобразование. Обозначим через g (t) минимальный аннулирующий многочлен этого преобразования. Разделим многочлен f (t) на g (t) с остатком f (t)= h (t) g (t)+ r (t). При подстановке матрицы A получим равенство f (A)= h (A) g (A)+ r (A)= r (A). Таким образом, вычисление значения многочлена от матрицы сводится к вычислению значению его остатка. Остаток от деления r (t) можно вычислить как интерполяционный многочлен Лагранжа - Сильвестра от корней минимального многочлена.

Ничего не изменится в проведенных рассуждениях, если вместо многочлена f (t) использовать произвольную функцию, значения которой, а также значения ее производных соответствующих порядков, определены на множестве корней минимального многочлена.

В некоторых случаях в качестве минимального многочлена берут характеристический многочлен.

Последовательность называется линейной рекуррентной, если существуют такие коэффициенты 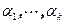, что для любого n справедливо равенство 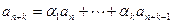. Для задания линейной рекуррентной последовательности, кроме ее коэффициентов, необходимо знать первые k членов , которые называются начальными условиями. Рассмотрим задачу выражения n-го члена последовательности через его номер и начальные условия.

Обозначим через вектор столбец, состоящий из k компонент 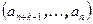, через 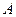— матрицу размерами 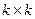вида 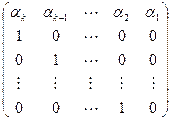. По правилу перемножения матриц имеем: 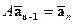. Многократным применением полученной формулы выводим . Задача вычисления n -го члена последовательности свелась, тем самым, к вычислению матрицы .

Характеристический многочлен 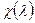матрицы А равен . Разделим многочлен на 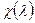с остатком. Пусть 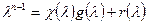, где - остаток от деления. Подставив вместо λ матрицу А, получим 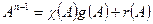. По теореме Гамильтона-Кэли каждая матрица является корнем своего характеристического уравнения, то есть 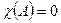, где 0 - нулевая матрица. Таким образом, , и задача вычисления свелась к вычислению многочлена r (λ).

Разложим многочлен 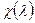на линейные множители , где . Для каждого неотрицательного j строго меньшего 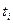справедливо равенство 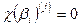, где - j -ая производная характеристического многочлена. Продифференцировав j раз равенство 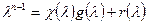и, подставив в него 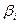, получим 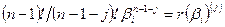. Этими условиями многочлен r (λ) степени k -1 определяется однозначно. В литературе задача вычисления многочлена по таким условиям носит название «интерполяционный многочлен Лагранжа-Сильвестра».

В качестве примера вычислим n -ый член линейной рекуррентной последовательности 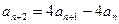, где . Положим . Характеристический многочлен равен 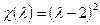. Остаток от деления на 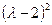удовлетворяет соотношениям и 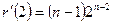. Единственный многочлен первой степени, удовлетворяющий этим условиям, равен . Таким образом, и .

Дата добавления: 2014-01-05