Примеры составления уравнений поверхностей

Пример 1. Введем в пространстве декартову прямоугольную систему коор­динат. Рассмотрим сферу S радиуса а с центром в точке С. Точка М (х,у, z) лежит на сфере S тогда и только тогда, когда длина отрезка СМ равна а (рис. 55) или тогда и только тогда, когда 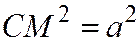или

.

В частности, уравнение сферы радиуса а с центром в начале координат имеет вид .

Пример 2. Введем в пространстве декартову прямоугольную систему координат Охуz, а кроме того - полярную, принимая положительную полуось Ох за полярную ось, за экваториальную плоскость - плоскость хОу, причем ориен­тируем ее треугольником (E ₁ и E ₂—масштабные точки осей Ох и Оу), а за зенитную ось - ось Оz. Рассмотрим сферу S радиуса а с центром в начале координат. Возьмем на этой сфере произвольную точку М (х,у,z), обозначим ее долготу и широту соответственно через u и 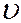(рис. 56).

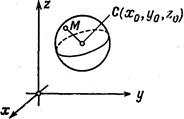Рис. 55

Рис. 56

Тогда (см. § 19, формулы (1)) ; таковы параметрические уравнения рассматриваемой сферы S. Криволинейные координаты точки М - это ее долгота и и широта 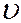. Область D изменения параметров и, 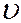такова:

Заметим, что сферу S в сферических координатах можно записать уравне­нием 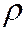=а.

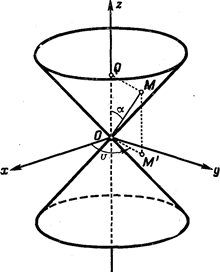Пример 3. Составим уравнение прямой круговой конической поверх­ности К, вершина которой находится в начале декартовой прямо-угольной системы координат, а острый угол между образующими поверхности и осью Оz равен .

Пусть М (х,у,z) - произвольная точка поверх-ности К; тогда рассто­яние MQ от этой точки М до оси Оz равно расстоянию М'O от про­екции М' (х,у, 0) точки М (х,у,z) в плоскость хОу до начала координат (рис. 57), т. е. .

С другой стороны, , а так как , то из последних соотношений находим , откуда .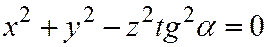

Обратно, если координаты некоторой точки М (х,у,z) удовлетворяют послед­нему уравнению, то , откуда 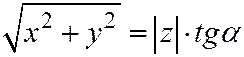или , а значит, точка М лежит на прямой, проходящей через начало координат и наклоненной к оси Оz под углом 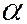, т. е. точка М лежит на поверхности конуса К.

Наряду с декартовой прямоугольной системой координат введем поляр­ную, как это сделано в § 19 (и в предыдущем примере). Обозначим через и расстояние от точки М до начала координат, а через 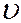- долготу точки М. Тогда

.

Однако этими параметрическими уравнени-ями не задается вся поверхность К, (так как ). Для задания параметрическими уравнениями всей поверхности К следует считать, что u принимает все действительные значения. Таким образом, область D изменения параметров и и 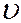такова: . (D)

При таком выборе области D изменения параметров и и 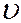предыдущие уравнения являются параметрическими уравнениями поверхности К.

Заметим, что часть поверхности К, соответствующая неотрицательным значениям и (т. е. одна полость конической поверхности К.), в сферических координатах может быть записана ура­внением вида ,

Рис. 58

а обе полости, т. е. вся поверхность К - двумя уравнениями:

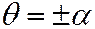
(знак + соответствует "верхней" части поверхности К, знак - "нижней").

Пример 4. Докажем, что уравнени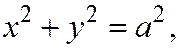е где , в декартовой прямоугольной системе координат является уравнением прямой круговой цилиндрической поверхности П с образующими, параллельными оси Оz, причем плоскость хОу пересекает эту поверхность по окружности С ра­диуса а с центром в начале координат.

В самом деле, координаты точки М (х,у,z) удовлетворяют уравнению 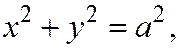тогда и только тогда, когда координаты М' (х,у, 0) проекции точки М на плоскость хОу удовлетворяют этому уравнению, а это значит, что точка М лежит на поверхности, заданной уравнением 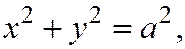тогда и только тогда, когда ее проекция М' на плоскость хОу лежит на окружности С: (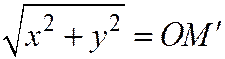). Значит, 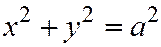есть уравнение цилиндрической поверхности П, описанной выше (рис. 58).

Дата добавления: 2014-01-05