Исследование формы эллипса

Так как в каноническое уравнение эллипса координаты х и у входят в четной степени (именно во второй), то если на эллипсе

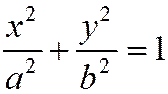(1)

лежит точка М (х, у), т. е. координаты этой точки удовлетворяют уравнению (1), то на том же эллипсе лежат точк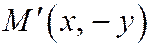и и 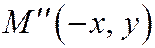, симметричные с точкой М относительно осей Ох и Оу, и точка 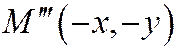, симметричная с точкой М относительно начала координат. Поэтому оси координат Ох и Оу для

эллипса, заданного каноническим уравнением (1) являются осями симметрии, а начало координат – центром симметрии. Из уравнения эллипса 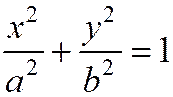следует, что для координат любой его точки имеют место соотношения

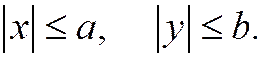
Геометрически это значит, что эллипс расположен внутри прямоугольника, сторонами которого являются прямые

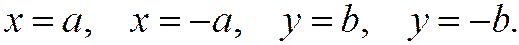
Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Таким образом, эллипс (1) имеет 4 вершины: , , , .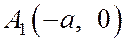

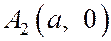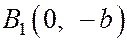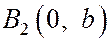Полуосью эллипса называется отрезок (а также длина этого отрезка), одним концом которого является центр симметрии эллипса, а другим – одна из его вершин; а называется большей полуосью эллипса, а b – меньшей полуосью.

Отрезок 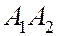- большая ось эллипса.

Отрезок 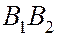- меньшая ось эллипса.

Замкнутая линия является выпуклой, если любая прямая пересекает ее не более чем в двух точках. Эллипс есть выпуклая замкнутая линия, так как, решая уравнение (1) эллипса совместно с уравнением прямо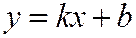й или 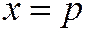, получим уравнение второй степени относительно х или у, значит, любая прямая пересекает эллипс не более чем в двух точках.

Итак, эллипс – замкнутая выпуклая линия, имеющая центр симметрии и две (взаимно перпендикулярные) оси симметрии.

Условимся уравнение 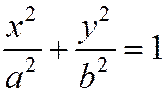называть каноническим уравнением эллипса и в том случае, когда а = b и когда a < b.

В случае а = b уравнение примет вид

,

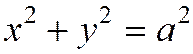т.е. является уравнением окружности радиуса а с центром в начале координат. Таким образом, мы рассматриваем окружность как частный случай эллипса. Этот частный случай соответствует совпадению фокусов 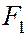и 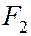с центром окружности.

В случае а < b большей полуосью будет b, а меньшей - а. Фокусы будут расположены на оси Оу на расстоянии 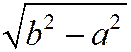от центра эллипса.

Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:

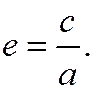
Так как 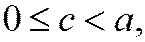то 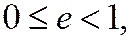т. е. эксцентриситет эллипса есть неотрицательное число, меньшее единицы.

Отметим, что 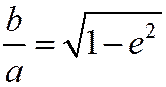(поскольку ).

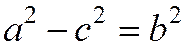Следовательно, эксцентриситет определяется отношением полуосей эллипса, и, обратно, отношение полуосей эллипса определяет его эксцентриситет.

Если эксцентриситет равен нулю е = 0, то а = b и эллипс является окружностью. Чем ближе эксцентриситет е к 1, тем меньше 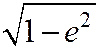и, значит, тем меньше отношение меньшей полуоси к большей. Таким образом, эксцентриситет характеризует степень «вытянутости» эллипса.

Вспоминая формулы:

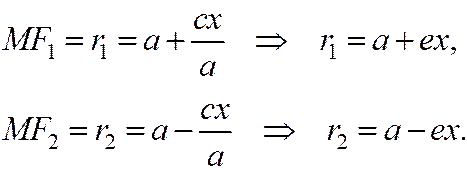
Дата добавления: 2014-01-05