Основные операции над векторами

Так мы будем называть операции сложения векторов, взятия противоположного вектора, умножения вектора на скаляр и вычитания.

Сначала определим операцию сложения двух направленных отрезков. Эта опера­ция не всегда определена. Она определена тогда и только тогда, когда конец первого от­резка совпадает с началом второго.

Определение 1. Суммою двух направленных отрезков (при выполнении вышепри­ведённого условия) называется направленный отрезок, начало которого совпадает с нача­лом первого данного отрезка, а конец − с концом второго.

Запишем это определение в виде формулы. Пусть даны два направленных отрезка: (A, B) и (C, D). Как сказано выше, их сумма существует в том и только том случае, когда B = C. Пусть это условие выполнено; тогда второй отрезок есть (B, D). Определение 1 можно теперь записать так:

(A, B) + (B, D) = (A, D).

Это правило сложения можно назвать правилом треугольника. Я его называю также правилом сокращения внутренних букв: всякий раз, когда у нас встречается выра­жение вида (A, B) + (B, D) (внутренние буквы совпадают), я могу заменить его на (A, D), т. е. внутренние буквы как бы сокращаются, остаются только внешние. Этим правилом можно пользоваться чисто формально, не обращаясь каждый раз к чертежу.

Теперь мы хотим определить сумму двух векторов. Вначале договоримся о неко­торой терминологии. Если дан вектор a, т. е. множество эквивалентных между собой на­правленных отрезков, и (A, B) − один из них, то мы будем говорить, что (A, B) есть один из представителей вектора a. Далее, представитель всегда можно выбрать так, чтобы его на­чало совпадало с любой наперёд заданной точкой. (В такой ситуации мы будем говорить, что мы прикладываем данный вектор к этой точке.) Точнее говоря, мы имеем

Предложение 1. Пусть дан вектор a и точка A (на плоскости или в пространстве). Тогда существует, и притом единственная, такая точка B, что направленный отрезок (A, B) является представителем вектора a (другими словами, 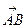= a).

Итак, пусть даны два произвольных вектора a и b (на плоскости или в простран­стве). Возьмём произвольный представитель вектора a, например, (A, B). Приложим век­тор b к точке B, т. е. найдём такой представитель (B, C) вектора b, что его начало совпа­дает с точкой B. Сложим теперь направленные отрезки (A, B) и (B, C), т. е. перейдём к от­резку (A, C), а от него к соответствующему вектору.

Определение 2. Вектор, полученный в результате вышеописанной процедуры, на­зывается суммою двух данных векторов a и b и обозначается a + b.

Заметим, что в отличие от суммы двух направленных отрезков сумма двух векто­ров, как это видно из описанной процедуры, всегда существует.

Возникает, однако, другой вопрос: однозначно ли определяется описанный выше вектор (сумма)? Если я возьму другой представитель первого вектора, то не получится ли у меня в конце другой вектор в качестве суммы? Оказывается, нет, получится другой на­правленный отрезок, но он будет соответствовать тому же самому вектору. В этом смысле наше определение 2 является, как говорят, корректным. Его корректность эквивалентна, очевидна, следующему утверждению.

Предложение 2. Если (A, B) ~ (A ¢, B ¢), а (B, C) ~ (B ¢, C ¢), то соответствующие суммы направленных отрезков (A, C) и (A ¢, C ¢) также будут эквивалентны.

Это предложение мы оставим без доказательства.

Заметим, что для сложения векторов также справедливо правило сокращения внут­ренних букв, а именно:

+=.

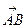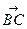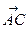Это непосредственное следствие определения и корректности суммы векторов, а также правила сокращения внутренних букв для направленных отрезков.

Предложение 3. Для любого вектора a имеет место равенство a + 0 = a.

Доказательство. Пусть (A, B) − произвольный представитель вектора a, а в каче­стве представителя нулевого вектора возьмём (B, B). Тогда

a + 0 = 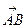+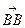==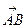 a, QED[3].

Рассмотрим теперь два свойства только что введённой операции сложения:

1) (a + b) + c = a + (b + c) (ассоциативность);

2) a + b = b + a (коммутативность).

Теорема 1. Сложение векторов ассоциативно и коммутативно.

Доказательство. Пусть даны векторы a, b и c. Выберем по представителю для этих трёх векторов, причём для a возьмём произвольный представитель (A, B), вектор b прилóжим к точке B, т. е. возьмём его представитель вида (B, C), а вектор c − к точке C, т. е. в качестве его представителя возьмём направленный отрезок (C, D). Имеем:

(a + b) + c = (+) += +=;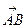

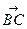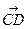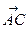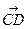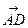a + (b + c) = + (+ ) =+=,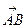

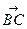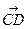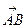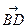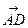т. е. мы доказали, что (a + b) + c = a + (b + c), QED.

Упражнение. Коммутативность докажите самостоятельно.

Теперь я хочу ввести ещё одну операцию − взятие противоположного вектора (или переход к противоположному вектору). Сделаем это сначала для направленных от­резков.

Определение 1. Если (A, B) − данный направленный отрезок, то противополож­ным к нему направленным отрезком (обозначение: −(A, B)) назовём отрезок (B, A).

Эта операция всегда возможна (в отличие от сложения). Довольно очевидно, что если два направленных отрезка эквивалентны, то противоположные к ним также будут эквивалентны. Это означает корректность следующего определения:

Определение 2. Если a − произвольный вектор, то противоположным к нему (обо­значение: − a) называется вектор, соответствующий направленному отрезку, противопо­ложному какому-нибудь представителю вектора a.

Другими словами, −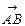= 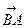. Ясно, что a + (− a) = 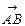+ (−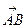) = 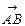+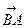= = 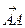= 0. Ясно также, что − 0 = 0 и что |− a | = | a |[4].

Введём теперь операцию умножения на скаляры, т. е. на действительные числа. Сначала сделаем это для направленных отрезков. Пусть (A, B) − направленный отрезок, λ − произвольный скаляр. Если A = B или λ = 0, то положим λ(A, B) = (A, A). В противном случае однозначно определена несущая прямая для (A, B). Если λ > 0, то отложим на не­сущей прямой от точки A в сторону точки B отрезок, равный по длине λ| AB |. Мы получим точку C. Теперь направленный отрезок (A, C) объявляем результатом умножения (A, B) на λ: λ(A, B) = (A, C). Если же λ < 0, то полагаем λ(A, B) = −(−λ)(A, B). Очевидно, что во всех случаях |λ(A, B)| = |λ|| AB |.

Теперь можно перейти к векторам. Пусть даны вектор a и скаляр λ. Выбираем про­извольный представитель (A, B) данного вектора a и вектор, соответствующий направлен­ному отрезку (A, C), построенному выше, объявляем результатом умножения λ на a. До­статочно очевидна корректность такого определения. Ясно также, что всегда |λ a | = |λ|| a |. Заметим также, что (−1) a = − a. и что −(− a) = a.

Определение 3. Две прямые называются коллинеарными, если они параллельны или совпадают.

Определение 4. Два ненулевых вектора называются коллинеарными, если их несу­щие прямые коллинеарны[5]. Обозначение: a || b. Нулевой вектор считается коллинеарным любому вектору.

Ясно, что вектор λ a всегда коллинеарен вектору a.

Предложение. Если a || b и b ≠ 0, то существует такое λ Î R, что a = λ b. Более того, это число (скаляр) λ определяется единственным образом.

Доказательство. Рассмотрим вектор s = 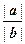b. Вычислим его длину:

| s | = |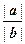 b | = |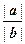|| b | =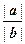| b | = | a |.

Таким образом, векторы s и a имеют одинаковую длину и, очевидно, коллинеарны (они оба коллинеарны вектору b). Векторы s и b сонаправленны, т. к. коэффициент 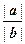неотрица­телен. Если a и b также сонаправленны, то в этом случае, очевидно, s = a. В про­тивном случае (т. е. если a и b противоположно направлены) векторы − a и s, очевидно, сонаправленны, имеют одинаковую длину и коллинеарны. Значит, они равны, т. е. a = − s. Таким образом, в первом случае можно взять λ = 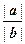, во втором случае можно положить λ = 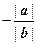, QED.

Единственность коэффициента λ докажем несколько позже.

Определение 5. Пусть даны два произвольных вектора a и b. Их разностью a − b называется вектор x, удовлетворяющий соотношению (уравнению)

x + b = a. (1)

Теорема. Разность двух данных векторов всегда существует и единственна.

Доказательство. Сначала докажем единственность. Пусть два вектора x ₁ и x ₂ удовлетворяют уравнению (1); тогда

x ₁ + b = x ₂ + b;

(x ₁ + b) + (− b) = (x ₂ + b) + (− b);

x ₁ + (b + (− b)) = x ₂ + (b + (− b));

x ₁ + 0 = x ₂ + 0;

x ₁ = x ₂.

Докажем теперь, что разность любых двух данных векторов a и b всегда сущест­вует. В самом деле, достаточно указать какое-либо решение уравнения (1) и проверить, что оно действительно является решением. Указываю: вектор x = a + (− b). Проверяем:

x + b = (a + (− b)) + b = a + ((− b) + b) = a + 0 = a,

QED.

Дата добавления: 2014-01-05