Расстояние от точки до плоскости

Условия параллельности и перпендикулярности

1°. Условие компланарности двух плоскостей

Пусть даны две плоскости:

A ₁ x + B ₁ y + C ₁ z + D ₁ = 0, n ₁ = { A ₁; B ₁; C ₁} ≠ 0;(1)

A ₂ x + B ₂ y + C ₂ z + D ₂ = 0, n ₂ = { A ₂; B ₂; C ₂} ≠ 0. (2)

Когда они компланарны (т. е. параллельны или совпадают)? Очевидно, это будет тогда и только тогда, когда их нормальные векторы коллинеарны. Применяя критерий компла­нарности, получаем

Предложение 1. Две плоскости компланарны тогда и только тогда, когда вектор­ное произведение их нормальных векторов равно нулевому вектору:

[ n ₁, n ₂] = 0.

2°. Условие совпадения двух плоскостей

Предложение 2. Плоскости (1) и (2) совпадают тогда и только тогда, когда все че­тыре их коэффициента пропорциональны, т. е. существует такое число λ, что

A ₂ = λ A ₁, B ₂ = λ B ₁, C ₂ = λ C ₁, D ₂ = λ D ₁. (3)

Доказательство. Пусть условия (3) выполнены. Тогда уравнение второй плоскости может быть записано так:

λ A ₁ x + λ B ₁ y + λ C ₁ z + λ D ₁ = 0.

λ ≠ 0, иначе было бы A ₂ = B ₂ = C ₂ = D ₂ = 0, что противоречит условию n ₂ ≠ 0. Следова­тельно, последнее уравнение эквивалентно уравнению (1), а это означает, что две плоско­сти совпадают.

Пусть теперь, наоборот, известно, что данные плоскости совпадают. Тогда их нор­мальные векторы коллинеарны, т. е. существует такое число λ такое, что

A ₂ = λ A ₁, B ₂ = λ B ₁, C ₂ = λ C ₁.

Уравнение (2) можно теперь переписать в виде:

λ A ₁ x + λ B ₁ y + λ C ₁ z + D ₂ = 0.

Умножим уравнение (1) на λ, получим равносильное уравнение первой плоскости (т. к. λ ≠ 0):

λ A ₁ x + λ B ₁ y + λ C ₁ z + λ D ₁ = 0.

Возьмём какую-нибудь точку (x ₀, y ₀, z ₀) из первой (а следовательно, и второй) плоскости и подставим её координаты в последние два уравнения; получим верные равен­ства:

λ A ₁ x ₀ + λ B ₁ y ₀ + λ C ₁ z ₀ + D ₂ = 0;

λ A ₁ x ₀ + λ B ₁ y ₀ + λ C ₁ z ₀ + λ D ₁ = 0.

Вычитая из верхнего нижнее, получим D ₂ − λ D ₁ = 0, т. е. D ₂ = λ D ₁, QED.

3°. Условие перпендикулярности двух плоскостей

Очевидно, для этого необходимо и достаточно, чтобы нормальные векторы были перпендикулярны.

Предложение 3. Две плоскости перпендикулярны тогда и только тогда, когда ска­лярное произведение нормальных векторов равно нулю:

(n ₁, n ₂) = 0.

Пусть дано уравнение плоскости

Ax + By + Cz + D = 0, n = { A; B; C } ≠ 0,

и точка M ₀ = (x ₀, y ₀, z ₀). Выведем формулу расстояния от точки до плоскости:

Возьмём произвольную точку Q = (x ₁, y ₁, z ₁), лежащую в данной плоскости. Её ко­ординаты удовлетворяют уравнению плоскости:

Ax ₁ + By ₁ + Cz ₁ + D = 0.

Заметим теперь, что искомое расстояние d равно абсолютной величине проекции вектора на направление вектора n (здесь мы берём проекцию как числовую величину, а не как вектор). Далее применяем формулу для вычисления проекции:

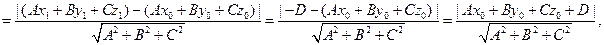
QED.

Аналогичная формула справедлива для расстояния d от точки M ₀ = (x ₀, y ₀) плоско­сти до прямой, заданной общим уравнением Ax + By + C = 0:

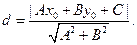
Дата добавления: 2014-01-05