Определение силы давления на наклонную стенку

О

h α

y

h_C

h_D

A dω

C y_C

α X

D y_D

Y

Рассмотрим силу давления жидкости на плоскую поверхность, наклоненную к горизонту под углом α. Давление со стороны жидкости в каждой точке этой наклонной поверхности будет разное в соответствии с глубиной погружения. Для определения силы давления, действующего со стороны жидкости на всю наклонную поверхность, определим сначала силу давления в какой-либо произвольной точке, и затем полученное выражение проинтегрируем. Расставим координатные оси. Ось Оy направим вдоль наклонной поверхности, начало координат возьмем в точке пересечения свободной поверхности с наклонной. Ось Ох развернем на 90⁰ в плоскости чертежа. В плоскости хОy отобразим наклонную поверхность. Сила давления в точке А будет равна

dP = pdω = (p + ρgh)dω.

P = p₀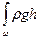ω +dω

P = p₀ω +ρg sinαdω

Статический момент площади относительно любой оси, лежащей в точй же плоскости, равен произведению этой площади на расстояние до центра тяжести от оси момента.

dω = y_C ω

P = p₀ω +ρg y_C ω sinα

P = p₀ω +ρg h_C ω

y_С – координата центра тяжести фигуры

ω – площадь фигуры

h_C – глубина погружения центра тяжести

Для того, чтобы определить силу давления жидкости на плоскую стенку необходимо давление в центре тяжести этой фигуры умножить на площадь.

Сила давления со стороны жидкости на наклонную поверхность будет приложена в точке, которая называется центром давлений.

Для определения координаты y_D центра давления воспользуемся теоремой о результирующем давлении. Момент результирующей силы равен сумме моментов ее составляющих.

Py_D = dP y

Для простоты записи будем рассматривать только избыточное давление.

P = ρg h_C ω; dP = ρg h dω;

y_D = 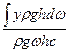₌ y_C + J₀/y_cω

Момент инерции некоторой площади относительно оси равен моменту инерции проходящей через центр тяжести и параллельный этой оси (в нашем случае Ох_ равен произведению площади на квадрат расстояния между этими осями.

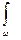y² dω = J₀ + ωy_C

Сила давления на горизонтальное дно равно весу этой жидкости в объеме цилиндра основанием которого служит эта площадь.

ω ω ω

Дата добавления: 2014-01-05