Свойства бинарных отношений

Задание отношений с помощью фактор множества.

Задание отношений в виде графа.

Матричный способ задания отношений.

При матричном способе задания бинарных отношений используют матрице смежности и матрицу инциденций . Матрица смежности строится следующим образом. Перенумеруем элементы множества 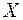целыми числами от 1 до 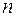: . Построим квадратную матрицу размером 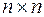. Её строка соответствует элементу множеств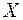а , а 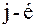столбец соответствует элементу множества 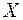. На пересечении строки и 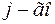столбца ставится единица, если в 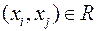, или в другой форме . Общее правило задания матрицы смежности бинарного отношения 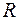можно формально записать:

Матрица смежности содержит всю информацию о том, для каких пар элементов из 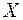выполнено отношение 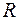. Произвол состоит в выборе нумерации на множестве 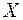. Является очевидным, что можно выбрать различных нумераций и, соответственно, матриц, описывающих данное отношение. Если задана матрица размером 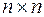из нулей и единиц и выбрана нумерация на множестве 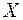, то тем самым на этом множестве задаётся некоторое отношение 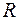. 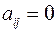Матрица смежности , для которой все , , задаёт пустое отношение 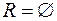, которое не выполняется ни для одной пары. Матрица смежности , для которой все , , задаёт полное отношение 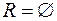, которое выполняется ни для всех пар. Особую роль играют матрицы , элементы которой принимают следующие значения:

В этом случае символ называется символом Кронекера по имени математика, впервые его употребившего. Этой матрице соответствует диагональное отношение 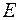, или отношение равенства. Соотношение 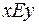выполняется, есл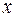и и 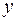─ один и тот же элемент. Матрица имеет вид:

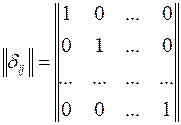
Существует также антидиагональное отношение, элементы которого принимают значения . Для пустого, полного, диагонального и антидиагонального отношений имеет место следующее свойство: их матрицы смежности не зависят от выбора нумерации элементов множества. Иначе говоря, если отношение таково, что при любом выборе нумерации элементов множества 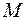их матрицы смежности совпадают, то 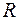является либо пустым, либо полным, либо диагональным, либо антидиагональным.

Существует ещё и другой важный способ задания бинарных отношений, заданных на конечных множествах. Изобразим элементы конечного множества 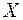точками на плоскости. Если выполнено соотношение (или 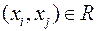), то проведём стрелку от 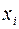к . Если выполняется (или 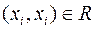), то нарисуем петлю, выходящую из 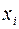и входящую в эту же точку. Такая фигура называется ориентированным графом, а сами точки ─ вершинами графа (рис. 2.19.).

При графическом способе задания бинарных отношений пустому отношению соответствует граф без стрелок и петель. Диагональное отношение изображается графом, в котором присутствуют только петли. Полное отношение изображается полным графом, где каждая его вершина соединена со всеми другими вершинами, в том числе и сама с собой. Граф есть геометрическое изображение бинарного отношения аналогично тому, как график есть геометрическое изображение функции. Геометрический язык полезен лишь тогда, когда граф достаточно прост. Изучать же сложные графы с большим числом вершин удобнее в терминах отношений.

Прежде, чем изложить способ задания бинарных отношений с помощью фактор множества, введём понятие окрестности единичного радиуса. Рассмотрим множество 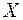с заданным на нём бинарным отношением .

Определение.

Окрестностью единичного радиуса элемента называется множество 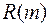, задаваемое следующей высказывательной формой:

.

Является бесспорным, что окрестность единичного радиуса представляет собой не что иное, как образ элемента носителя бинарного отношений.

Определение.

Множество окрестностей единичного радиуса, взятых для всех элементов носителя 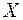бинарного отношения , называется фактор множеством множества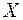по отношению 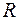и обозначается .

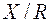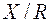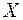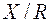Таким образом, фактор множество можно представить как объединение окрестностей единичного радиуса, взятых для всех элементов множества : . Фактор множество полностью определяет отношение .

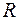Рассмотрим свойства, которыми могут обладать бинарные отношения. Допустим, что на некотором множестве 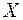как на носителе задано бинарное отношение , . Произвольное бинарное отношение может обладать следующими свойствами.

1. Свойство рефлексивности , т.е. любой элемент из множества 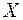находится сам с собой в отношении 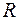. Свойство рефлексивности можно записать в форме соотношений: в инфиксной форме, в префиксной форме , в постфиксной форме .

2. Свойство антирефлексивности т.е. любой элемент из множества 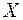не может находиться сам с собой в отношении 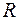. Или в форме соотношений: в инфиксной форме , в префиксной форме 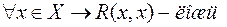, в постфиксной форме .

2. Свойство симметричности , т.е. если элемент носителя 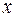находится в отношении 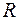с элементом носителя 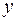, то и элемент 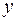находится в отношении 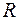с элементом 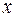. В форме соотношений это свойство можно записать: в инфиксной форме , в префиксной форме , в постфиксной форме .

3. Свойство антисимметричности

, т.е. если элемент 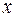находится в отношении 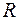с элементом 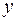и одновременно элемент 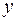находится в отношении 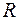с элементом 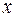, то эти элементы совпадают. В форме соотношений это свойство выглядит следующим образом: в инфиксной форме

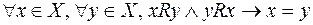, в префиксной форме 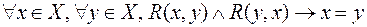, в постфиксной форме .

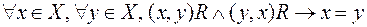4. Свойство несимметричности 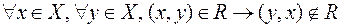, т.е. если элемент 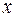находится в отношении 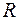с элементом 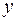, то элемент 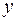не находится в отношении 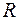с элементом 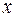. В форме соотношений это свойство можно записать: в инфиксной форме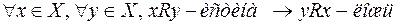, в префиксной форме , в постфиксной форме .

5. Свойство транзитивности 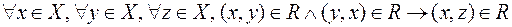, т.е. для любых элементов 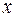,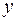и 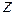из множества 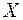если элемент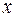находится в отношении 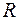с элементом 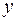, а элемент 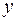находится в отношении 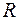с элементом 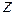, то элемент 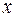находится в отношении 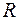с элементом 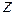. В форме соотношений это свойство выглядит следующим образом: в инфиксной форме

, в префиксной форме , в постфиксной форме .

6. Свойство антитранзитивности 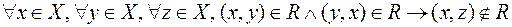, или в форме соотношений: в инфиксной форме , в префиксной форме .

Перечисление свойств бинарных отношений совсем не означает, что все бинарные отношения ими обладают. В зависимости от присущих бинарным отношениям свойств они подразделяются на виды, которые будут рассмотрены далее.

Дата добавления: 2014-01-05