Пересечение прямой линии с плоскостью или поверхностью

Построение точек пересечения прямой линии с плоскостью или поверхностью в проекциях с числовыми отметками аналогично по решению такой же задачи в других методах проецирования, а именно:

1) прямая заключается во вспомогательную секущую плоскость–посредник;

2) строится линия пересечения плоскости посредника с заданной плоскостью (поверхностью);

3) отмечается точка (точки) пересечения построенной линии с заданной прямой.

Рассмотрим решение задач на примерах. Отметим, что в качестве посредника можно использовать вертикальную плоскость (метод профилей) или плоскость общего положения (метод горизонталей).

Пример. Определить точку пересечения прямой АВ с плоскостью Г (рис. 15.9).

Решение. Для решения задачи через заданную прямую проведена горизонтально проецирующая плоскость ∆, пересекающая заданную плоскость по прямой МN. С помощью замены плоскостей проекций построены дополнительная проекция прямой АВ и линии пересечения двух плоскостей. Вначале определена дополнительная проекция К^/ искомой точки пересечения, а затем и горизонтальная проекция.

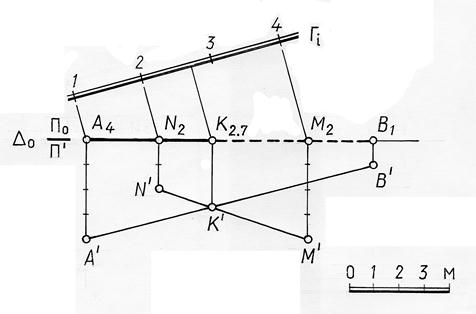
Рис. 15.9

Решение этой задачи можно выполнить с помощью плоскости общего положения.

Пример. Определить точку пересечения прямой АВ с плоскостью Г (рис. 15.10).

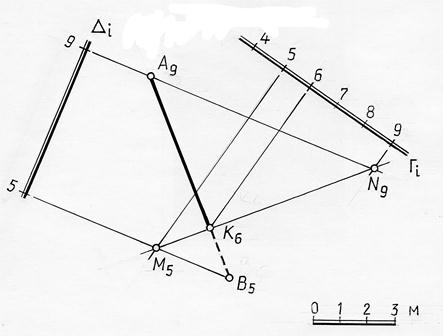
Рис. 15.10

Решение. Через прямую АВ проводится произвольная вспомогательная плоскость общего положения ∆ _i, заданная горизонталями (h₉, h₅).

Горизонтали вспомогательной плоскости проводятся через точки А и В так, чтобы они в пределах чертежа пересекали горизонтали, имеющие те же отметки заданной плоскости Г_i.

Затем строится линия пересечения вспомогательной плоскости ∆ _i с плоскостью Г – прямая МN. Точка К – точка пересечения прямой АВ и линии MN – есть искомая точка пересечения прямой с плоскостью Г. Отметка точки К определяется по масштабу уклона плоскости Г.

Пример. Измерить расстояние от точки А до плоскости Г (рис. 14.11).

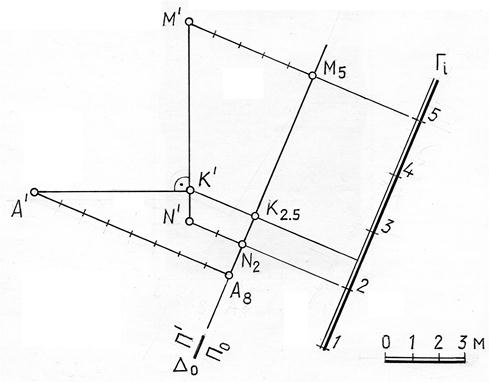
Рис. 15. 11

Решение. Из точки А опускаем перпендикуляр на плоскость Г, находим точку К – точку пересечения этого перпендикуляра с плоскостью Г, а затем – натуральную величину отрезка прямой АК.

Ранее известно, что горизонтальная проекция перпендикуляра к плоскости составляет прямой угол с одноименными горизонталями этой плоскости. Что то же, проекция прямой, перпендикулярной плоскости, параллельна масштабу падения этой плоскости. Следовательно, для решения задачи через точку А₈ проведена прямая параллельная масштабу падения плоскости Г_i. Чтобы найти точку пересечения построенного перпендикуляра с плоскостью, через него проведена вспомогательная горизонтально проецирующая плоскость ∆, пересекающая заданную плоскость по прямой МN. С помощью замены плоскостей проекций построена дополнительная проекция линии пересечения двух плоскостей МN, которая является линией наибольшего ската плоскости Г и перпендикуляра к плоскости АК, который перпендикулярен к любой прямой этой плоскости, в том числе и к линии наибольшего ската. А^/К^/ – является натуральной величиной перпендикуляра АК, а точка К – основанием перпендикуляра.

Пример. Построить точки пересечения прямой с топографической поверхностью (рис. 15.12, 15.13).

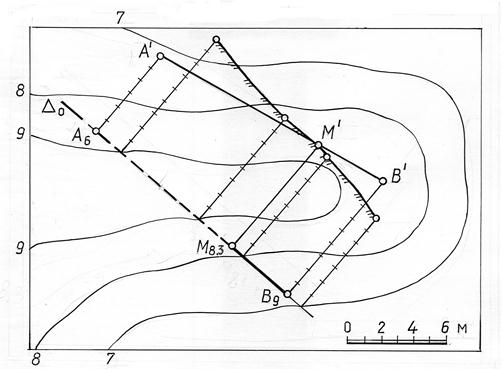
Рис.15.12

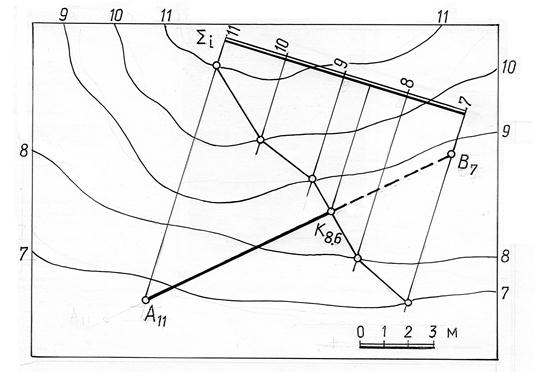
Рис. 15.13

Решение. Через прямую АВ (рис.15.13) проводится горизонтально проецирующая плоскость ∆ и строится профиль этого сечения топографической поверхности. А^/B^/ - проекция прямой в сечении. Точка пересечения проекции А^/B^/ c профилем топографической поверхности определяет проекцию М^/ – точки пересечения заданной прямой с топографической поверхностью. Проведя линию проекционной связи, определяем горизонтальную проекцию этой точки.

Если на чертеже задана проградуированная проекция прямой, то для решения задачи рационально использовать плоскость-посредник общего положения, как показано на рис. 15.14. Для определения точки пересечения прямой АВ с топографической поверхностью через прямую АВ проведена плоскость общего положения å. Вспомогательная плоскость задана на чертеже с помощью горизонталей, которые проведены так, чтобы они в пределах чертежа не пересекали горизонтали с одинаковыми отметками топографической поверхности. Затем построено сечение топографической поверхности плоскостью-посредником и отмечена точка пересечения построенной линии и заданной прямой АВ, точка К – есть искомая точка пересечения прямой с топографической поверхностью. Отметка точки К определяется по масштабу уклона вспомогательной плоскости å.

Дата добавления: 2014-01-05