Однородные уравнения

Уравнения с разделяющими переменными.

Уравнения вида 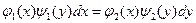, в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от X и только от Y называется уравнением с разделяющими переменными. Путём деления на произведение 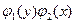оно приводится к уравнению с разделёнными переменными:

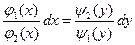
Общий интеграл этого уравнения имеет вид

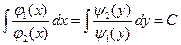
Пример 2.1. Найти частное решение уравнения 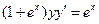, удовлетворяющее начальному условию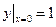

Решение. Имеем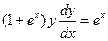

Разделяя переменные, получаем

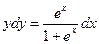
Интегрируя, найдём общий интеграл

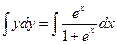
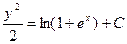(1)

Полагая X=0 и Y=1, будем иметь 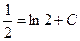, откуда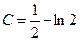

Подставляя в (1) найденное значение C, получаем частное решение ;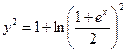

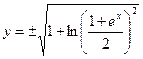
Из начального 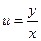условия следует, что 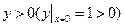поэтому перед корнем берём знак плюс. Итак, искомое частное решение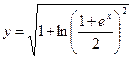

Функция 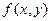называется однородной функцией своих аргументов измерения n, если справедливо тождество

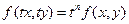
При n=0 имеем функцию нулевого измерения.

Дифференциальное уравнение вида 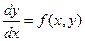называется однородным относительно x и y, если 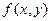есть однородная функция своих аргументов нулевого измерения.

Однородное уравнение всегда можно представить в виде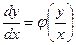

Вводя новую искомую функцию 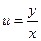, имеем уравнение с разделяющимися переменными

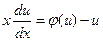
Пример 3.1. Решить уравнение

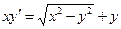
Решение. Запишем уравнение в виде

так что данное уравнение оказывается однородным относительно x и y.

Положим 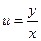или 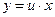, тогда 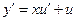. Подставляя в уравнение выражение для и 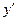, получаем

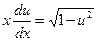
Разделяем переменные ;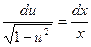

,

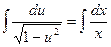
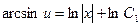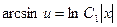
т.к. 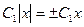, то, обозначая 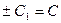, получаем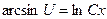

Заменяя 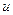на 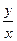, будем иметь общий интеграл ,

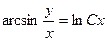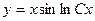
Дата добавления: 2014-01-05