Основной постулат метрологии

Понятие о шкалах измерений

Погрешности измерений

Любое измерение предполагает получение информации о размере физической величины путем сравнения неизвестного размера измеряемой величины с известным и выражением первого через второй.

Простейший способ получения такой информации, состоит в сравнении по принципу «Что больше (меньше)». Расположение по этому принципу размеры измеряемых величин образуют шкалу порядка. Особенно широкое распространение такие шкалы получили в областях, где измерения с помощью технических средств не достигли высокого совершенства (в гуманитарных науках, искусстве и т.д.). недостатками таких шкал является неопределенность интервалов между опорными точками (например шкала вида: неудовлетворительно, удовлетворительно, хорошо, отлично). Результаты измерений по этим шкалам нельзя складывать, вычитать, перемножать, делить.

Более совершенными в этом отношении являются шкалы, составленные из строго определенных интервалов – шкалы интервалов. По шкале интервалов можно судить не только о том, что один размер больше другого, но и о том, на сколько больше, т.е. на шкале интервалов можно выполнять такие математические действия как сложение и вычитание (временные шкалы, шкала температур Цельсия и т.п.).

Но, если на шкале интервалов выбрать точку, в которой размер физической величины равен нулю (не принимается равным нулю, а действительно равен нулю), то по этой шкале уже можно отсчитывать абсолютное значение размера и определять не только, на сколько этот размер больше или меньше другого, но и во сколько раз он больше или меньше. Эта шкала называется шкалой отношений.

Шкала отношений является наиболее совершенной из всех рассмотренных шкал. На ней можно выполнять операции сложения, вычитания, деления и умножения. Большинство физических величин электрической природы измеряется с использованием этой шкалы.

Измерение по шкале отношений предполагает сравнение неизвестного размера с известным и выражение первого через второй в кратном или дольном отношении. Эта операция сравнения неизвестного значения с известным и выражения первого через второе в кратном или дольном отношении запишется следующим образом:

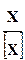
где 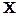– неизвестный размер, 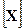- известный размер.

В реальных условиях измерения такое сравнение не всегда удается выполнить, т.к в большинстве случаев в измерении участвуют различного рода преобразователи измеряемой величины. Тогда операция сравнения выглядит как определение отношения

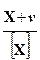
в случае аддитивного воздействия преобразователя, или как определение отношения

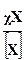
в случае мультипликативного воздействия преобразователя, т.е. мы измеряем уже не саму неизвестную величину, а результат ее преобразования преобразователем.

Само сравнение результата преобразования 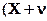или 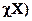с известным размером происходит под воздействием множества случайных факторов (электромагнитных помех, температуры окружающей среды, влажности, вибрации, напряжения питания измерительного прибора, состояния субъекта измерения – оператора и т.п.).

Ограничиваясь для простоты рассмотрения только аддитивным воздействием преобразователей, совместное влияние этих факторов можно учесть слагаемым 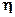. Тогда получим следующее уравнение измерения по шкале отношений

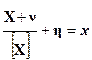
где 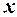–результат отсчет по шкале.

Это уравнение является математической моделью измерения (по шкале отношений).

При повторении измерительной процедуры из – за случайного характера 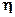x получается все время разным. Это фундаментальное положение является законом природы. На основании опыта практических измерений и формулировано утверждение, называемое основным постулатом метрологии: отчет является случайным числом.

После выполнения измерения величины 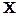в уравнении остаются два неизвестных 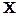и 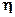. Неслучайная соответствующая 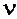должна быть известна до измерения. Слагаемое 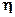, является случайным, не может быть известно в принципе. Поэтому определить значение измеряемой величины

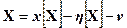(3.6)

невозможно.

В выражении 3.6 первое слагаемое в правой части называется показанием, а две последних суммарной поправкой.

Приняв известный размер 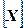за размер единицы измеряемой величины, можно записать выражение 3.6 в виде:

X =x +c

Дата добавления: 2014-01-05