
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение необходимого объема выборки
|
|
|
|
Очень важное значение имеет определение оптимальной численности выборки, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения. При увеличении численности выборки ошибка выборки уменьшается. Но так как отобранные единицы для обследования часто разрушаются, то нормы отбора единиц в выборку должны быть оптимальными. Оптимальную численность выборки можно получить из формул ошибок выборки.
Таблица 8.4
Формулы определения оптимальной численности выборки
| Способ отбора | Для средней | Для доли |
| Собственно-случайный повторный | 
| 
|
| Случайный и механический бесповторный | 
| 
|
| Типологический бесповторный | 
| 
|
| Серийный бесповторный с равновеликими сериями | 
| 
|
Формулы показывают, что с увеличением предполагаемой ошибки выборки значительно уменьшается необходимый объём выборки.
Для расчета объёма выборки нужно знать дисперсию. Она может быть заимствована из проводимых ранее обследований данной или аналогичной совокупности или можно провести специальное выборочное обследование небольшого объёма.
Пример 2: На предприятии в порядке случайной бесповторной выборки были опрошены 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь (табл. 8.5).
Таблица 8.5
Распределение рабочих по размеру среднего месячного дохода
| Месячный доход, тыс. руб. | 15–17 | 17–19 | 19–21 | 21–23 |
| Число рабочих, чел. |
Определить:
1) среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0,997;
2) долю рабочих предприятия, имеющих месячный доход 19 тыс. руб. и выше, гарантируя результат с вероятностью 0,954;
3) необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 200 руб.
|
|
|
Решение:
1) Определим среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0,997.
Дано:
n = 100 чел.
N = 1000 чел.
P = 0,997
 Найти:
Найти:

| Решение: для определения интервала среднемесячного дохода работников данного предприятия в генеральной совокупности необходимо знать величину предельной ошибки выборки 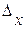 и размер среднемесячного дохода рабочих по данным выборочного обследования и размер среднемесячного дохода рабочих по данным выборочного обследования 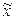 .
Предельная ошибка выборки определяется по формуле .
Предельная ошибка выборки определяется по формуле 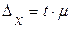 . Она зависит от величины коэффициента доверия t и средней ошибки выборки . Она зависит от величины коэффициента доверия t и средней ошибки выборки 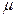 .
Поскольку P = 0,997, то (по табл. 8.2) t = 3.
Был произведен случайный бесповторный отбор, по табл. 8.3 выбираем формулу для расчета средней ошибки выборки для средней: .
Поскольку P = 0,997, то (по табл. 8.2) t = 3.
Был произведен случайный бесповторный отбор, по табл. 8.3 выбираем формулу для расчета средней ошибки выборки для средней:
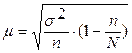 , где , где 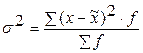 – дисперсия по выборке.
Размер среднемесячного дохода рабочих по данным выборочного обследования – дисперсия по выборке.
Размер среднемесячного дохода рабочих по данным выборочного обследования 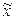 определим по формуле средней арифметической взвешенной: определим по формуле средней арифметической взвешенной: 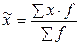 .
Дополнительные расчеты проведем в следующей таблице: .
Дополнительные расчеты проведем в следующей таблице:
Зная t и
Тогда интервал среднего месячного дохода рабочих данного предприятия будет таким:
|
Ответ: среднемесячный размер дохода у работников данного предприятия с вероятностью 0,997 находится в пределах от 18,08 тыс. руб. до 18,92 тыс. руб.
2) Определим долю рабочих предприятия, имеющих месячный доход 19 тыс. руб. и выше, гарантируя результат с вероятностью 0,954.
Дано:
n = 100 чел.
N = 1000 чел.
P = 0,954
 Найти:
Найти:

| Решение: для определения интервала доли рабочих, имеющих месячный доход 19 тыс. руб. и выше необходимо, знать величину предельной ошибки выборки доли 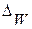 и долю рабочих с таким среднемесячным доходом по данным выборки W.
Предельная ошибка выборки определяется по формуле и долю рабочих с таким среднемесячным доходом по данным выборки W.
Предельная ошибка выборки определяется по формуле 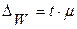 . Она зависит от величины коэффициента доверия t и средней ошибки выборки . Она зависит от величины коэффициента доверия t и средней ошибки выборки 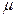 .
Поскольку P = 0,954, то (по табл. 8.2) t = 2.
Был произведен случайный бесповторный отбор, по табл. 8.3 выбираем формулу для расчета средней ошибки выборки для доли: .
Поскольку P = 0,954, то (по табл. 8.2) t = 2.
Был произведен случайный бесповторный отбор, по табл. 8.3 выбираем формулу для расчета средней ошибки выборки для доли:
 , где W – доля рабочих предприятия, имеющих среднемесячный доход 19 тыс. руб. и выше по выборке.
Выборочная доля определяется отношением числа единиц, обладающих изучаемым признаком m к общему числу единиц выборочной совокупности n, или , где W – доля рабочих предприятия, имеющих среднемесячный доход 19 тыс. руб. и выше по выборке.
Выборочная доля определяется отношением числа единиц, обладающих изучаемым признаком m к общему числу единиц выборочной совокупности n, или 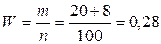 .
Тогда средняя ошибка доли равна .
Тогда средняя ошибка доли равна
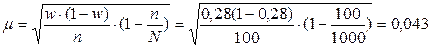 .
Зная t и .
Зная t и 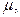 определим величину предельной ошибки выборки для доли: определим величину предельной ошибки выборки для доли:
 .
Тогда интервал доли рабочих с месячным доходом 19 тыс. руб. и выше в генеральной совокупности будет таким: .
Тогда интервал доли рабочих с месячным доходом 19 тыс. руб. и выше в генеральной совокупности будет таким:
 ; ;
 ; ;
 . .
|
Ответ: доля рабочих предприятия, имеющих месячный доход 19 тыс. руб. и выше, с вероятностью 0,954 находится в пределах от 19,4% до 36,6%.
|
|
|
3) Определим необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 200 руб.
Дано:
N = 1000 чел.
P = 0,954
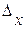 = 200 руб. = 200 руб.
 Найти:
n –?
Найти:
n –?
| Решение: необходимая численность выборки для определения среднего месячного дохода определяется по формуле (по табл. 8.4):
 .
По условию задачи известны: при вероятности Р = 0,954 t = 2 (см. табл. 8.2); .
По условию задачи известны: при вероятности Р = 0,954 t = 2 (см. табл. 8.2);
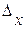 = 0,2 тыс. руб.; = 0,2 тыс. руб.; 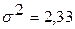 (по данным предыдущей выборки). (по данным предыдущей выборки).
 чел. чел.
|
Ответ: чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 200 руб., должны быть обследованы 189 чел.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 2011; Нарушение авторских прав?; Мы поможем в написании вашей работы!
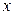
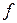
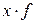
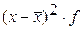
 тыс. руб.
тыс. руб.
 тыс. руб.
тыс. руб.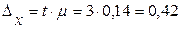 тыс. руб.
тыс. руб.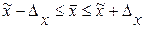 ;
;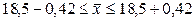 ;
;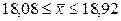 .
.