Наращение простыми процентами

Тема 2. ПРОСТЫЕ ПРОЦЕНТЫ

1. Наращение простыми процентами.

2. Переменные ставки и реинвестирование.

Ссудо-заемные операции, составляющие основу коммерче­ских вычислений, имеют давнюю историю. Именно в этих опе­рациях и проявляется, прежде всего, необходимость учета вре­менной ценности денег. Несмотря на то, что в основе расчетов при анализе эффективности ссудо-заемных операций заложены простейшие на первый взгляд схемы начисления процентов, эти расчеты многообразны ввиду вариабельности условий финансо­вых контрактов в отношении частоты и способов начисления, а также вариантов предоставления и погашения ссуд.

Предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. При этом выделяется некоторый основной интервал времени, который называется базовым. Поскольку стандартным временным интервалом в финансовых операциях является один год, наиболее распространен вариант, когда этот год берется в качестве базового интервала и процентная ставка устанавлива­ется в виде годовой ставки, подразумевающей однократное на­числение процентов по истечении года после получения ссуды. 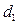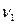В этом случае будем опускать индекс у процентной ставки (как в дальнейшем и у , ) и писать просто (соответственно 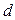, 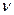). Известны две основные схемы дискретного начисления, т.е. начисления процентов за фиксированные в договоре интер­валы времени:

- схема простых процентов (simple interest);

- схема сложных процентов (compound interest).

Схема простых процентов предполагает неизменность вели­чины, с которой происходит начисление. Пусть исходный инве­стируемый капитал равен 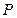; требуемая доходность - (в десятичных дробях). Считается, что инвестиция сделана на ус­ловиях простого процента, если инвестированный капитал ежегодно увеличивается на величину 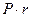. Таким образом, размер 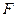инвестированного капитала через лет будет равен:

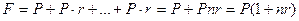, (2.1)

т.е. проценты начисляются на одну и ту же величину капитала в течение всего срока.

Выражение (2.1) называется формулой наращения по про­стым процентам или формулой наращения простыми процен­тами, а множитель - множителем наращения (accumulation factor) или коэффициентом наращения простых процентов. Очевидно, множитель наращения равен индексу роста капитал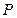а за лет.

Легко видеть, что приращение капитала

(2.2)

пропорционально сроку ссуды и ставке процента, т.е. можно сделать вывод, что доход инвестора растет линейно вместе с . Величина дохода называется процентом или, часто, процентным платежом.

На практике процентная ставка может зависеть от величи­ны исходного капитала 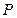: с увеличением капитала 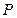увеличива­ется и устанавливаемая ставка . Например, если инвестируется капитал до 20 тыс. тенге, то устанавливается одна ставка процен­та, если более 20 тыс. тенге - то другая (превышающая предыдущую).

Отметим, что если ставка дана в процентах, то при исполь­зовании формулы (2.1) ставку нужно выразить в десятичных дробях.

Пример:

Найти величину процента и наращенную сумму за трехлет­ний кредит в 20 тыс. тенге, взятый под 9%.

Здесь тыс. тенге, года, . Тогда

тыс. тенге,

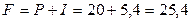тыс. тенге

Обратим внимание на размерности величин, определяющих процентный платеж (2.2). Так как 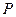измеряется в денежных единицах (например, рублях), - в единицах времени (годах), то размерностью является 1/(единица времени) (1/(год)), т.е. размерности и всегда должны быть согласованы. Таким образом, либо должно измеряться в годах, либо с изменением размерности (например, не годы, а кварталы) ставка процента должна отражать рост за новую единицу времени (за квартал).

С этих позиций наращение по простым процентам в случае, когда продолжительность финансовой операции не равна целому числу лет (например, меньше года), определяется по формуле

(2.3)

где - продолжительность финансовой операции в днях;

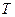- количество дней в году.

Тогда 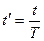- продолжительность финансовой операции, уже измеряемая в годах (т.е. в данной ситуации ).

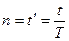Для наглядности формулу (2.3) можно записать следующим образом: 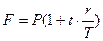, т.е. дробь представляет собой дневную ставку, а произведение 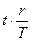- ставку за дней.

Следует отметить, что в обозначениях является процентной ставкой за время 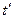и тогда (2.3), естественно, примет вид, аналогичный (1.7):

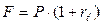
Так как 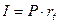, то наращение по формуле (2.3) и, конечно, по (2.1) происходит процентами «со 100».

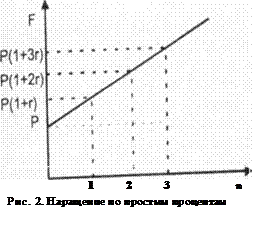
Сравнивая (2.1) и (2.3), можно сделать вывод, что формула (2.1) носит общий характер, поскольку в качестве можно рассматривать любое положительное число, необязательно целое (напомним, что при этом условии формула (2.1) получена). Таким образом, (2.1) представляет собой зависимость наращенной суммы от времени, знание которой, в частности, позволяет на практике установить правила досрочного расторжения договора. Эта зависимость является линейной, и ее график имеет вид прямой линии с тангенсом угла наклона, численно равным процентам 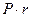за один год (рис. 2).

Наращение по простым процентам применяется при обслу­живании сберегательных вкладов с ежемесячной выплатой про­центов и вообще в тех случаях, когда проценты не присоединя­ются к сумме долга, а периодически выплачиваются кредитору. Простые проценты применяют и при выдаче широко распро­страненных краткосрочных ссуд, т.е. ссуд, предоставляемых на срок до одного года с однократным начислением процентов.

Пример:

Клиент поместил в банк вклад в сумме 3,5 тыс. тенге под 24% годовых с ежемесячной выплатой процентов. Какую сумму кли­ент будет получать каждый месяц?

Так как в этих условиях Р = 3,5 тыс. тенге, года, 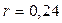, то по формуле (2.2)

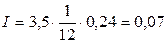тыс. тенге

Заметим, что если бы клиент не брал деньги, то к его вкладу каждый месяц прибавлялась бы сумма в 0,07 тыс. тенге, поскольку начисление происходит по простым процентам. Если обозначить через 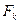наращенную сумму через 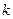месяцев, то последовательность 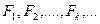образует арифметическую прогрессию с первым членом 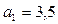и разностью 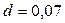. Естественно, аналогичный результат можно доказать и в общем случае.

Определяя продолжительность финансовой операции, приня­то день выдачи и день погашения ссуды считать за один день, В зависимости от того, чему берется равной продолжительность года (квартала, месяца), получают два варианта процентов:

точный процент (exact interest), определяемый исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);

обыкновенный процент (ordinary interest), определяемый исходя из приближенного числа дней в году, квартале и месяце (соответственно 360, 90, 30).

При определении продолжительности периода, на который выдана ссуда, также возможны два варианта:

принимается в расчет точное число дней ссуды (расчет ведется по дням);

принимается в расчет приблизительное число дней ссу­ды (исходя из продолжительности месяца в 30 дней).

Для упрощения процедуры расчета точного числа дней поль­зуются специальными таблицами (одна для обычного года, вто­рая для високосного), в которых все дни в году последовательно пронумерованы. Продолжительность финансовой операции оп­ределяется вычитанием номера первого дня из номера последне­го дня (см. приложение 2).

В том случае, когда в расчетах используется точный процент, берется и точная величина продолжительности финансовой опе­рации; при использовании обыкновенного процента может при­меняться как точное, так и приближенное число дней ссуды. Таким образом, расчет может выполняться одним из трех спо­собов:

обыкновенный процент с приближенным числом дней, обозначаемый как 360/360 (применяется в Германии, Да­нии, Швеции);

обыкновенный процент с точным числом дней, обозна­чаемый как 365/360 или АСТ/360 (Бельгия, Франция);

точный процент с точным числом дней, обозначаемый как 365/365 или ACT/ACT (Великобритания, США).

В российской практике можно встретиться с различными схемами начисления процентов. Эффект же от выбора того или иного способа иного способа зависит от значительности суммы, фигурирую­щей в процессе финансовой операции. Но и так ясно, что ис­пользование обыкновенных процентов с точным числом дней ссуды, как правило, дает больший результат, чем применение обыкновенных процентов с приближенным числом дней ссуды.

Пример:

Предоставлена ссуда в размере 7 тыс. тенге 10 февраля с по­гашением 10 июня под 20% годовых (год невисокосный). Рас­считать различными способами сумму к погашению ( F).

Величина уплачиваемых за пользование ссудой процентов зависит от числа дней, которое берется в расчет. Точное число дней определяется, например, по табл. 1 в приложении 2: 161-41=120 дн. Приближенное число дней ссуды равно: 18 дней февраля (59- 41) + 90 дней (по 30 дней трех месяцев: март, ап­рель, май) + 10 дней июня = 118 дн.

Возможные варианты возврата долга:

1. В расчет принимаются точные проценты и точное число дней ссуды:

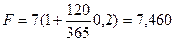тыс. тенге

2. В расчет принимаются обыкновенные проценты и точное число дней:

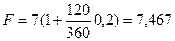тыс. тенге

3. В расчет принимаются обыкновенные проценты и приближенное число дней:

тыс. тенге

Пример:

Найти величину процентного платежа за 60-дневный кредит в 200 тыс. тенге, взятый под 6% годовых, если расчет ведется способом 360.360.

По формуле (2.2) получим:

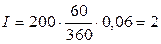тыс. тенге

Этот пример показывает, как надо применять так называемое, "правило 6% -60 дней" (6% - 60 day rule), которое значительно упрощает вычисление процента. Согласно этому правилу процентный платеж (процент) может быть найден просто делением исходного капитала Р на 100.

"Правило 6% - 60 дней" в определенном смысле можно применять и при произвольных значениях и , если предварительно преобразовать формулу (2.2), умножая и деля процентный платеж на соответствующие числа следующим образом:

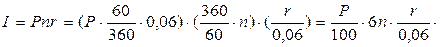
В мировой финансовой практике при расчете процента ис­пользуют и другие величины. Пусть 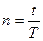в обозначениях фор­мулы (2.3). Тогда (2.2) можно записать в виде 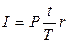. Поде­лив в правой части равенства числитель и знаменатель дроби на , получим

(2.4)

где произведение 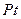называется процентным числом, a 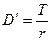называется процентным ключом, постоянным делителем или дивизором.

Очевидно, что при одной и той же ставке , но при различ­ном принимаемом количестве дней в году (Т = 360 или Т = 365) будет разным и дивизор.

Дивизор численно равен такому количеству рублей (долларов или любых других денежных единиц), с которого при ставке процента получается 1 тенге дохода в день. Это можно пояснить таким образом: тенге получается с 1 тенге за 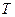дней, поэтому 1 тенге за то же время получается с капитала , а чтобы иметь 1 тенге дохода каждый день, необходимо взять в 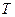раз больше капитала, т.е. .

Пример:

Вычислить процент с капитала 2,4 тыс. тенге, отданного в долг по ставке 20% годовых на срок с 5 марта по 21 сентября того же года, если расчет ведется способом 365/365.

Обозначим Р = 2,4 тыс. тенге Число дней находим либо пря­мым подсчетом, либо по таблице: дней. Так как Т = 365 и , то и по формуле (2.4) получим

тыс. тенге, т.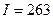е. тенге

Если ставка выражается в процентах, то, очевидно, дивизор определяется выражением . Именно в таком виде он, как правило, встречается в литературе по коммерческим вычис­лениям XIX и начала XX вв. и называется постоянным делите­лем.

При вычислении процентного платежа не всегда известна ве­личина капитала Р. Возможны такие ситуации (например, в залоговых операциях), что известна либо только величина капи­тала, увеличенного на процентный платеж (т.е. P + I), либо уменьшенного на процентный платеж (т.е. Р - I).

Пусть известна величина F = Р + I, годовая ставка (в ви­де десятичной дроби) и длительность (выраженная в годах, необязательно натуральным числом) финансовой операции. Тогда 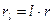будет процентной ставкой за время , и для на­хождения процентного платежа пользуемся формулой (1.10) вычисления процентов "на 100"

(2.5)

Если же известна величина 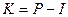, то для нахождения процентного платежа пользуемся формулой (1.11) вычисления процентов "во 100"

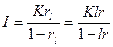(2.6)

Пример:

Найти величину дохода кредитора, если за предоставление в долг на полгода некоторой суммы денег он получил от заемщика в совокупности 6,3 тыс. тенге. При этом применялась простая процентная ставка в 10% годовых.

Обозначая 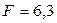тыс. тенге; года; 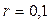по формуле (2.5) получим:

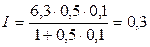тыс. тенге

В случае, когда срок финансовой операции выражен в днях и обозначен через , формулы (2.5), (2.6) после простых алгеб­раических преобразований соответственно примут вид:

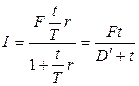(2.7)

(2.8)

Пример:

При обращении 6 июля в банк с целью получения кредита предприниматель получил 10 тыс. тенге Найти, какую сумму должен будет возвратить предприниматель, если долг необхо­димо вернуть 14 сентября того же года и начисленные простые проценты по ставке 12% годовых были удержаны банком в мо­мент предоставления кредита. Используется способ 365/360.

Вначале воспользуемся формулой (2.8) для определения про­центов, удержанных банком. Так как t = 70 дней, Т = 360 дней,

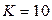, , тыс. тенге, то

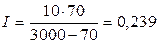тыс. тенге

Следовательно, предприниматель обязан возвратить долг в размере

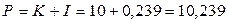тыс. тенге

В банках при обслуживании текущих счетов для начисления процентов часто используют величины 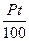, которые (так же, как и 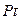) называются процентными числами. В этом случае формула для вычисления дивизора остается прежней: , но ставка в ней выражена в процентах.

Обычно сумма на счете часто меняется в результате поступ­лений или изъятий денежных сумм. Для того чтобы найти об­щую величину начисленных процентов за некоторый срок, вна­чале определяют процентные числа за каждый промежуток вре­мени, когда сумма на счете не менялась. Затем все процентные числа складываются и полученное значение делится на .

Пример:

Сберегательный счет был открыт 15 февраля, и на него была положена сумма в 5 тыс. тенге. В следующем квартале 10 апреля на счет поступили 3 тыс. тенге Затем 20 мая со счета были сняты 2 тыс. тенге, 1 сентября добавлена сумма в 1 тыс. тенге и 4 декабря счет был закрыт. Все операции осуществлялись в течение года (невисокосного). Определить сумму, полученную владельцем счета, если процентная ставка равнялась 12% годовых и приме­нялся способ 365/360.

Вначале определяем суммы, которые последовательно фик­сировались на счете: 5 тыс. тенге, 8(5 + 3) тыс. тенге, 6 (8 -2) тыс. тенге, 7 (6 + 1) тыс. тенге. Затем находим сроки хранения этих сумм. Они соответственно равны: 54 дня, 40 дней, 104 дня, 94 дня. Сумма процентных чисел составит:

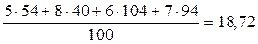
Дивизор в данном случае равен: D. Следователь­но, общая величина начисленных процентов составит: тыс. тенге, а владелец счета получит 7 + 0,624 = 7,624 тыс. тенге

Заметим, что процентные числа можно было вычислять и с несколько иным образом найденными сроками, а именно: для каждого поступления срок хранения определяется исходя из даты поступления и даты закрытия счета. Если происходило изъятие денег, то соответствующее процентное число берется со знаком минус. Тогда для 5 тыс. тенге - 292 дня, для 3 тыс. тенге - 238 дней, для 2 тыс. тенге - 198 дней и для 1 тыс. тенге - 94 дня. Находим (учитывая знаки) сумму процентных чисел:

,

т.е. получили такую же величину.

Дата добавления: 2014-01-05