Сложная учетная ставка

Тема 5. СЛОЖНЫЕ ПРОЦЕНТЫ

1. Сложная учетная ставка.

2. Непрерывное наращение и дисконтирование.

Рассмотрим ситуацию предварительного начисления сложно­го процента, т.е. когда сложный процент (например, за кредит или за продажу некоторого финансового документа до срока его погашения) начисляется в момент заключения финансового соглашения. В этом случае осуществляется операция дисконти­рования (учета) и применяется сложная учетная ставка (compounddiscount rate).

Предположим, что некоторое долговое обязательство на сумму 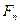и сроком погашения через лет продается (учитыва­ется) раньше срока с дисконтом по сложной годовой учетной ставке 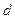. Если осуществить продажу за год до срока, то начис­ляются проценты и продавец получит сумму 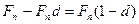. Если осуществить продажу за два года до срока погашения, то за один год проценты начисляются на 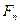, а за второй год - уже на сумму 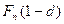, дисконтированную на предыдущем шаге, т.е. продавец получит сумму 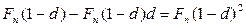и т.д. Если долговое обязательство продается за 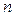лет до срока, то продавец получит сумму

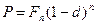(5.1)

где множитель 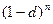называется дисконтным множителем.

Таким образом, представляет собой текущую (современ­ную) стоимость будущего платежа 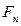. Дисконт 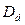равен вели­чине:

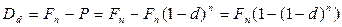(5.2)

По формуле (5.1) (как следует из пояснений этой формулы) сумма 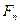учитывается из сложных процентов "со 100".

Пример:

Долговое обязательство на выплату 20 тыс. тенге со сроком погашения через 4 года учтено за 2 года до срока с дисконтом по сложной учетной ставке 8%. Найти величину дисконта.

Поскольку 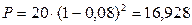тыс. тенге, то

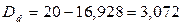тыс. тенге

Если срок , за который осуществляется дисконтирование, не является целым числом лет, то возможны следующие методы определения стоимости учтенного за 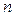лет капитала:

- использование сложной учетной ставки (применяется формула (5.1)):

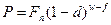, (5.3)

- использование смешанной схемы (применяется сложная учетная ставка для целого числа лет и простая учетная ставка - для дробной части года):

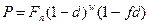, (5.4)

где 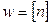- целое число лет;

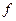- дробная часть года,

;

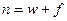
Конечно, при 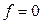формулы (5.3) и (5.4) совпадают меж­ду собой и с формулой (5.1).

Пример:

В условиях предыдущего примера долговое обязательство учтено за 27 месяцев до срока. Найти величину дисконта.

Обозначим 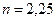; ; 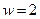; 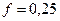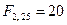. По формуле (5.3) получим:

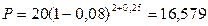тыс. тенге

и, следовательно,

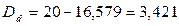тыс. тенге

Используя формулу (5.4), получим

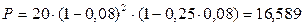тыс. тенге,

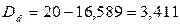тыс. тенге

Сравним между собой дисконтирование по простой и сложной учетным ставкам. Для этого достаточно сравнить множители дисконтирования 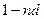и 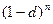, которые, очевидно, при 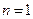совпадают и равны 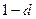. Можно доказать, что при 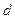, удовлетворяющих неравенству 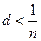, справедливы неравенства:

а) 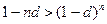, если ;

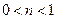б) , если .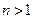

Таким образом, для лица, осуществляющего предварительное (антисипативное) начисление процентов, а следовательно, и дисконтирование:

- более выгодным является дисконтирование по сложной учетной ставке, если срок учета менее одного года;

- более выгодным является дисконтирование по простой учетной ставке, если срок учета превышает один год;

-дисконтирование в обоих случаях дает один и тот же результат, если срок учета равен одному году.

Полезно представлять себе, что с практической точки зрения условие 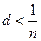на самом деле не является таким уж сильным ограничением. Так как для учетной ставки 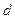справедливо 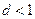, то при 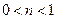условие 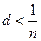автоматически выполняется. А если 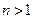, то неравенство б) формально справедливо и при 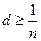, поскольку тогда 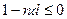, но всегда 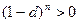. Однако на практике, при дисконтировании по простым процентам случай 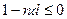приводит к абсурду.

Пример:

Определить дисконтированную сумму при учете 1 млн. тенге по простой и сложной учетным ставкам, если годовая учетная ставка равна 14% и учет происходит за 30 дней, 90 дней, 180 дней, 1 год, 5 лет, 7 лет. Полагать год равным 360 дням.

Получим следующие результаты расчетов:

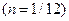
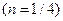
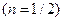
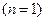
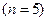
Способ дисконтирования	30 дней	90 дней	180 дней	1 год	5 лет	7 лет
Простая учетная ставка	0,988	0,965	0,93	0,86	0,3	0,02
Сложная учетная ставка	0,9875	0,9630	0,9274	0,86	0,4704	0,3479

Заметим, что дисконтирование по простой учетной ставке за срок более, чем 7,15 года приводит к недопустимым на практике величинам (будем получать отрицательные значения дисконтированных сумм). Однако учет по сложной учетной ставке всегда дает положительные дисконтированные величины. Например, при учете за 10 лет получим: 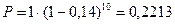млн. тенге.

Пусть дисконтирование происходит 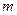раз в году и задана сложная годовая учетная ставка 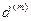(аналогичным образом, как и ранее для процентной ставки, при помощи верхнего индекса 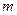указываем, сколько раз в течение года происходит дисконти­рование). Годовая учетная ставка 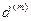называется номинальной (nominal discount rate), если в начале каждого периода длительностью 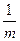осуществляется дисконтирование по ставке .

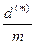В этих обозначениях формула (5.1) для определения стои­мости капитала, учтенного за лет при 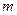- кратном дисконти­ровании в течение года, примет вид

(5.5)

Поскольку 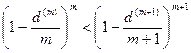, то с ростом числа дисконтирования в году величина учтенного капитала возрастает.

Пример:

Долговое обязательство на выплату 3 тыс. тенге со сроком по­гашения через 5 лет учтено за два года до срока. Определить полученную сумму, если производилось: а) полугодовое; б) по­квартальное дисконтирование по номинальной учетной ставке 12%.

В данном случае , ;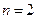

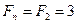а) так как 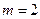, , 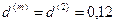то по формуле (5.5):

тыс. тенге;

б) так как , , 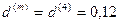то по формуле (5.5):

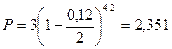тыс. тенге

Пусть в (5.5) не является целым числом. Это возможно тогда, когда антисипативное начисление процентов (или дисконтирование) осуществляется по внутригодовым подпериодам, но общий период не равен целому числу подпериодов. В этом случае можно использовать либо формулу:

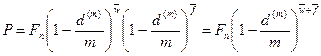(5.6)

либо формулу:

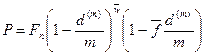(5.7)

где , , .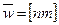

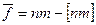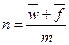Конечно, (5.6), по существу, является иной записью (5.5).

Пример:

Определить современное значение суммы в 4 тыс. тенге, если она будет выплачена через 2 года и 3 месяца и дисконтирование производилось по полугодиям по номинальной годовой учетной ставке 10%.

Полагаем 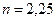года, 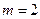. Тогда , ; , .

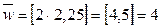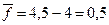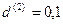Если использовать формулу (5.6), то

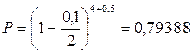тыс. тенге, что равно 793 тенге 88 тиын.

А если использовать формулу (5.7), то

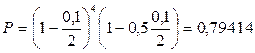тыс. тенге, что равно 794 тенге 14 тиын

Из равенства (5.5) определяется период 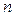, если известны значения всех остальных параметров:

(5.8)

Отсюда при 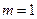, 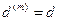получим формулу

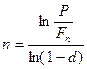(5.9)

которую, конечно, можно вывести и из (5.1).

Пример:

За долговое обязательство в 300 тыс. тенге банком было вы­плачено 200 тыс. тенге. За какое время до срока погашения было учтено это обязательство, если банком использовалась годовая сложная учетная ставка 8%?

Полагая 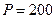, , 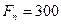, 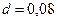по формуле (5.9) по­лучим:

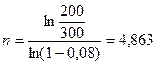года

Из равенства (5.5) можно найти величину номинальной учетной ставки (если известны значения остальных параметров)

,

а при 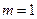, 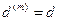эта формула примет вид

.

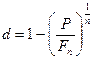Пример:

Вексель был учтен за полтора года до срока, при этом владе­лец векселя получил 0,8 от написанной на векселе суммы. По какой сложной годовой учетной ставке был учтен этот вексель?

Поскольку 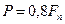„ 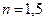, то 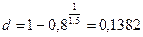, т.е. .

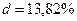Как и в случае процентной ставки, можно определить эф­фективную годовую учетную ставку 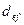, обеспечивающую переход от 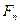к 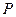при заданных значениях этих параметров и однократном дисконтировании. Поскольку согласно определе­нию в рамках одного года

,

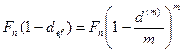то после простых преобразований получим

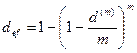(5.10)

Из (5.10) следует, что 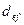уменьшается с ростом 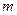(так как второе слагаемое в правой части равенства увеличивается). Во­обще можно показать, что при 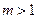справедливо неравенство 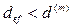, которое, естественно, объяснимо и из финансовых соображений.

Пример:

Рассчитать эффективную годовую учетную ставку при раз­личной частоте начисления дисконта и номинальной учетной ставке, равной 10%.

Используя формулу (5.10), для некоторых значений 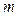ре­зультаты запишем в табличном виде:

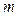
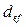
	0,10	0,0975	0,0963	0,0955	0,0952

Из формулы (5.10) можно найти соотношение для определе­ния номинальной учетной ставки, если известны 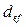и число 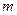дисконтирования в год:

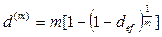(5.11)

Пример:

Определить номинальную ставку, если эффективная учетная ставка равна 9% и дисконтирование по сложной учетной ставке осуществляется ежемесячно.

В данном случае 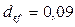и 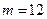, поэтому по (5.11):

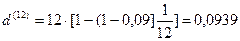, или .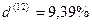

Используя эффективную учетную ставку, можно определить эквивалентные номинальные учетные ставк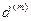и и 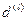как ставки, удовлетворяющие равенствам:

.

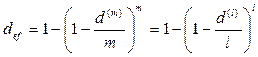Следует отметить, что эффективную годовую учетную ставку можно найти, не зная номинальной учетной ставки, а зная величину 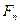и ее дисконтированную (каким-либо образом) за время сумму 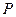. Поскольку согласно 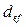можно записать 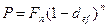, то

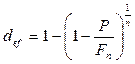(5.12)

Пример:

Долговое обязательство, равное 5 тыс. тенге со сроком погашения через 4 года было сразу же учтено в банке и владелец обязательства получил 4,2 тыс. тенге. Найти эффективную учетную ставку в этой сделке.

По формуле (5.12):

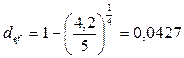, или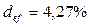

Сложная учетная ставка применяется не только для осуществления процесса дисконтирования. Разрешим равенство (5.1) относительно :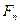

(5.13)

Равенство (5.13) называется формулой наращения сложными процентами по учетной ставке; множитель 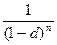- множителем наращения при начислении сложных антисипативных процентов; - коэффициентом наращения или сложным антисипативным коэффициентом. Естественно, множитель наращения равен индексу роста капитала 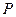за лет.

Формула (5.13) представляет собой формулу наращения сложными процентами «во 100». Действительно

,

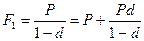т.е. 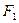является суммой первоначального капитала 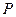и процентов «во 100» по отношению к 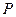. Поскольку

,

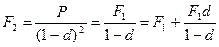то 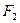является суммой капитала 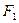(наращенного за год из капитала 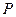) и процентов «во 100» по отношению к 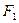и т.д.

Очевидно, что приращение капитала

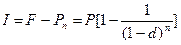(5.14)

не пропорционально ни сроку , ни ставке .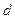

Заметим, что 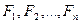, определяемые по формуле (5.13), образуют геометрическую прогрессию со знаменателем .

Так как при 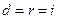справедливо неравенство 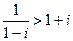(если, конечно, 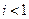, а для учетной ставки это всегда выполнено), то наращение по учетной ставке (5.13) происходит быстрее (что выгодно для кредитора), чем наращение по процентной ставке (3.1) (что выгодно для заемщика).

Покажем, как с помощью декурсивного и антисипативного способов начисления процентов можно пояснить, почему наращение процентами «во 100» (используя учетную ставку) доставляет существенно больший результат, чем наращение процентами «со 100» (используя процентную ставку).

Пусть на исходный инвестируемый капитал 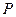начисляются проценты по ставке . При декурсивном способе в конце года инвестор получит сумму 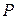и проценты 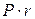"со 100", т.е. 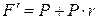. При антисипативном способе проценты 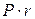начисляются в начале года, и пусть они сразу выдаются инве­стору, который тут же их инвестирует. На величину 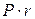на­числяются проценты и сразу выдаются инвестору, кото­рый немедленно их инвестирует, и т.д. Предположим (конечно, только теоретически), что эти действия повторяются неограни­ченное число раз, тогда инвестор получит величину:

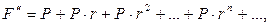
представляющую собой сумму членов геометрической прогрес­сии с неограниченным числом членов и знаменателем 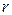. Таким образом, 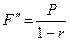, а это и есть наращение процентами "во 100".

Если наращение сложными процентами по учетной ставке происходит 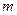раз в год, то формулу для определения наращен­ной суммы получим из равенства (5.5), разрешая его относи­тельно :

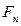(5.15)

причем с ростом частоты 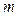начисления сложных процентов накопленная сумма 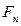уменьшается.

Пример:

По условиям финансового контракта на депозит в 400 тыс. тенге, положенный в банк на 3 года, начисляются проценты по сложной учетной ставке 9% годовых. Определить наращенную сумму, если начисление процентов производится: а) ежегодно; б) по полугодиям; в) ежемесячно.

Допустим .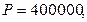

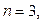
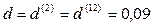а) по формуле (5.13):

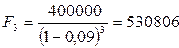тенге;

б) поскольку 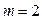, то используем (5.15):

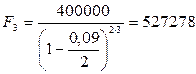тенге;

в) полагая 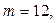по (5.15) получим:

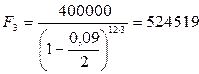тенге;

Полезно заметить, что в случаях б) и в) можно было, естест­венно, воспользоваться формулой (5.13), полагая число перио­дов равным соответственно 6 и 36, а учетные ставки - 4,5% (9%: 2) и 0,75% (9%: 12). Если бы наращение сложными про­центами осуществлялось с помощью процентной ставки, то для вариантов а), б), в) получили бы по формулам (3.1), (3.12) соот­ветственно значения: 518 012 тенге, 520 904 тенге, 523 458 тенге, т.е. с увеличением числа начислений процентов за год величина наращенной суммы возрастает. В противоположность этому с увеличением числа начислений процентов за год по сложной учетной ставке величина наращенной суммы убывает. Видно, что чем больше число наращений в течение года, тем меньше разница между итоговыми суммами, полученными декурсивным и антисипативным способами начисления процентов. Это и объяснимо, поскольку чем меньше период начисления, тем меньше отличие между понятиями "предварительный" и "последующий". Так, если 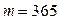(каждый день идет начисление сложных процентов), то применение учетной ставки дает 524 003 тенге, а такой же величины процентной ставки - 523 968 тенге, и разница между этими суммами равна всего 35 тенге

В некоторых ситуациях по условиям контракта предусматри­ваются плавающие учетные ставки. Пусть на периоды 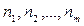установлены учетные ставки соответственно 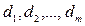. Тогда при наращении сложными процентами итоговая сумма за время 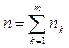(измеряя все периоды в одних единицах времени) определяется по формуле

(5.16)

Обозначим 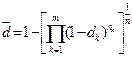, тогда (5.16) примет вид . Таким образом, на все время 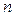можно установить вместо плавающих учетных ставок учетную ставку 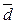, которая обеспечивает такой же результат, и при определении можно использовать формулу (5.13).

Если 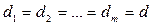, т.е. на весь период соглашения ус­тановлена постоянная ставка, то из (5.16) получаем (5.13).

Очевидно, формулой (5.16) можно пользоваться и в случае, когда периоды выражены в различных единицах времени при условии согласования их размерностей с размерностями соот­ветствующих учетных ставок.

Пример:

Вклад в размере 1000 тенге положен в банк сроком на 7 лет, причем предусмотрен следующий порядок начисления сложных процентов по плавающей учетной ставке: в первые два года - 8%, в последующие четыре года - 12%, а в оставшийся год - 15%. Найти наращенную сумму.

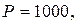
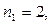
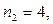
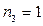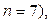
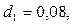
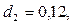
Полагаем (таким образом, 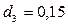и воспользуемся форму­лой (5.16):

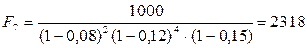тенге.

Такой же величины наращенная сумма получается и при ис­пользовании в течение 7 лет сложной учетной ставки

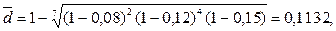или .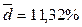

Дата добавления: 2014-01-05