Основные понятия и определения. ТЕМА 1. Дифференциальные уравнения

ТЕМА 1. Дифференциальные уравнения. Методы решения ОДУ первого порядка.

Определение1. Обыкновенным дифференциальным уравнением (ОДУ) называется уравнение, связывающее независимую переменную 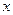, меняющуюся на некотором интервале числовой прямой , , 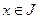независимую функцию и её производные .

В общем виде ОДУ можно записать так:

, где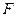- неизвестная функция от переменных.

Определение2. Порядком дифференциального уравнения называется максимальный порядок производной неизвестной функции, входящей в уравнение.

Определение3. Функция 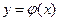называется решением дифференциального уравнения, если при подстановке в данное уравнение получается верное тождество.

(для .)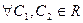

Таким образом, ОДУ имеют бесконечное множество решений.

Рассмотрим уравнение первого порядка:

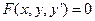(1)

Если это уравнение можно разрешить относительно 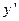, то мы получим уравнение вида 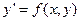(*), которое называется уравнением, разрешенным относительно производной. Простейшим видом такого уравнения является уравнение .

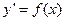Пусть 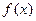- непрерывная на функция, тогда решение уравнения (*) будет иметь вид (2), где .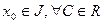

Как видим, уравнение тоже имеет бесконечное множество решений. Для того, чтобы выделить единственное решение, необходимо наложить дополнительное условие: , которое называется условием Коши. Тогда из формулы (2) найдем единственное решение

Рассмотрим дифференциальное уравнение 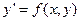(3)

с условием (4).

Уравнение (3) с условием (4) называется задачей Коши. Решить задачу Коши – значит найти решение уравнения (3), которое удовлетворяет начальному условияю (4).

Теорема ( существования и единственности решения задачи Коши )

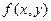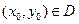Пусть функция в некоторой области непрерывна, точка и удовлетворяет в условию Липшица: (это условие равносильно тому, что непрерывна в ). Тогда существует единственное решение задачи Коши (3),(4) на промежутке .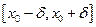

Замечание1: Геометрическая интерпретация теоремы: при выполнении условии теоремы через каждую точку 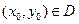проходит интегральная прямая и при том только одна (общему решению соответствует семейство интегральных прямых)

Замечание2. Из формулировки теоремы следует, что уравнение (3) имеет бесконечно много решений, зависящих от одной произвольной постоянной.

Пример:

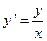
Общее решение этого уравнения . Тогда .

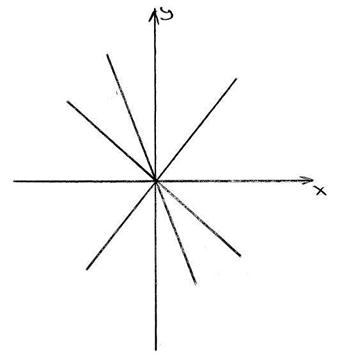
Если в данной точке условия теоремы нарушены, то через нее либо вообще не проходит ни одна интегральная прямая, либо проходит бесконечное множество интегральных кривых.

Замечание3. В уравнении (3) переменные 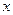и 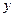неравноправны: 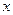-независимая переменная, а 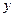- функция от 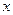, но во многих задачах, приводящих к уравнению (3), 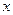и 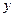могут быть равноправны. В этом случае дифференциальное уравнение записывают в дифференциалах:

(5)

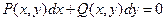(5’) – уравнение в дифференциалах.

§1.2. Уравнения с разделяющимися переменными.

Определение. Уравнением с разделяющимися переменными называется уравнение вида (1), где 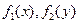- непрерывные на функции. Перепишем уравнение (1) в виде:

- уравнение с разделенными переменными.

(2)

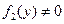В уравнении (2) фиксированы и . Формула (2) записывается в виде (2’), где 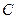- произвольная постоянная.

Однако формула (2) не дает всех решений уравнении (1), так как при её выводе мы делили на , которое может обращаться в ноль.

Таким образом, все решения уравнения (1) определяется формулой (2) или (2’) и нулями функции .

Пример:

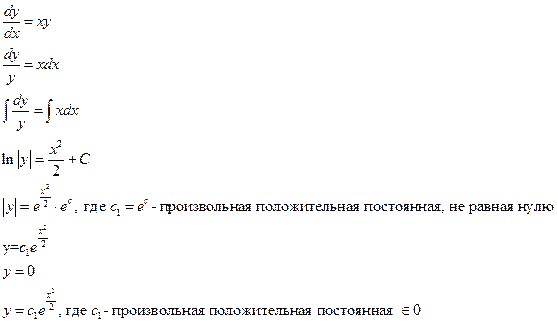
Замечание. К уравнению с разделяющимися переменными сводятся и уравнения вида:

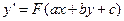
Заменим неизвестную функцию 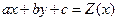, пусть

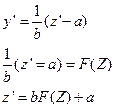
Так как в правой части стоит функция, зависящая только от 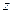, то полученное уравнение с разделяющимися переменными.

Пример:

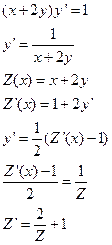
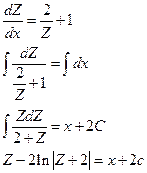
Вернемся к переменной :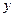

Дата добавления: 2014-01-05