Критерии устойчивости Гурвица и Рауса (алгебраические)

Необходимое и достаточное условие устойчивости системы управления без решения характеристического уравнения было сформулировано Гурвицем в виде неравенств [3]. Пусть характеристическое уравнение системы управления имеет вид:

b_o 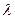ⁿ+ b₁ 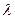^n-1+... + b_n = 0.

Тогда с учетом его коэффициентов может быть составлена матрица Гурвица:

При составлении матрицы Гурвица по диагонали записываются коэффициенты характеристического уравнения, начиная с b₁. Строки вправо от диагонали заполняются коэффициентами в порядке возрастания индексов, а слева – в порядке убывания. Несуществующие коэффициенты ассоциируются с нулем. Гурвиц доказал, что для выполнения условия устойчивости, то есть для расположения всех корней характеристического уравнения в левой полуплоскости, необходимо и достаточно, чтобы при b_o > 0 все определители Гурвица (определители диагональных миноров матрицы Гурвица)

₁ = b₁ > 0; 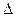₂ = det > 0;...

были положительными. Остановимся кратко на некоторых общих замечаниях. Вычисление определителей Гурвица высоких порядков непосредственным разложением их по элементам строки или столбца сопряжено с большим числом вычислений и неоправданной затратой времени, поэтому весьма полезны правила, упрощающие расчеты:

1) для расположения всех корней характеристического уравнения слева от

мнимой оси необходимо (но недостаточно), чтобы все коэффициенты b_i

были одного знака;

2) обращение в нуль определителя _i свидетельствует о появлении пары

чисто мнимых корней;

3) если все коэффициенты характеристического уравнения положительны, то

все вещественные корни (если они есть) отрицательны. Комплексные

корни при этом могут лежать и в правой полуплоскости;

4) если в последовательности b_0, b_1, b_2,…, b_n имеется одна перемена знака, то

имеется один корень, лежащий в правой полуплоскости. Если число

перемен знака равно N > 1, то число таких корней равно N;

5) критерий Гурвица удобно применять для уравнений не выше четвертой

степени. Для более высоких степеней целесообразнее использовать

алгоритм Рауса, ориентированный на использование ЭВМ в расчетах.

Критерий устойчивости Рауса [4] — один из методов анализа линейной стационарной динамической системы на устойчивость. Наряду с критерием Гурвица (который часто называют критерием Рауса-Гурвица) является представителем семейства алгебраических критериев устойчивости. К достоинствам метода относится простая реализация на ЭВМ, а также простота анализа для систем небольшого (до 3) порядка. К недостаткам можно отнести ненаглядность метода, по нему сложно судить о степени устойчивости, о её запасах.

Метод работает с коэффициентами характеристического уравнения системы. Пусть W(s)— передаточная функция системы:

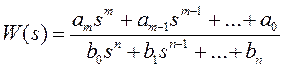
(1.28)

B(s)— характеристический полином системы.

Критерий Рауса представляет собой алгоритм, по которому составляется специальная таблица, в которой записываются коэффициенты характеристического полинома таким образом, что:

1. В первой строке записываются коэффициенты уравнения с чётными индексами в порядке их возрастания.

2. Во второй строке — с нечётными.

3. Остальные элементы таблицы определяется по формуле:

(1.29)

где

(1.30)

i >= 3 — номер строки, 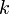— номер столбца.

4. Число строк таблицы Рауса на единицу больше порядка характеристического уравнения

Формулировка критерия Рауса:

Для устойчивости линейной стационарной системы необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса с_1,1, с_1,2, с_1,3,… были одного знака. Если это не выполняется, то система неустойчива.

Составим таблицу, которая называется таблицей Рауса.

Таблица 1.2

Коэфф. 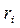i->k	i	Столбец
-						…
-						…
						…
						…
						…
…	.	…	…	…	…

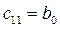
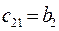
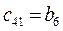
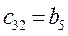
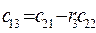
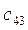
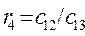
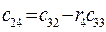
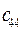
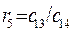
Cледствием критерия Рауса является следующее утверждение: если хотя бы один коэффициент характеристического уравнения отрицателен, то система неустойчива, а если равен нулю, то это свидетельствует о появлении пары чисто мнимых корней, что характерно для неустойчивых систем управления, либо находящихся на границе устойчивости. Число отрицательных коэффициентов равно числу правых полюсов. В таблице Рауса для упрощения расчетов элементы строк можно делить или умножать на положительные величины. Таблица, реализующая алгоритм Рауса, удобна для программирования на ЭВМ, поэтому с помощью этого метода можно исследовать на устойчивость системы высокого порядка, а также исследовать влияние на устойчивость отдельных параметров системы.

Дата добавления: 2014-01-05