
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод простой итерации Якоби
 |
Метод Гаусса обладает довольно сложной вычислительной схемой. Кроме того, при вычислениях накапливается ошибка округления, что может привести к недостаточно точному результату. Рассмотрим метод простой итерации Якоби, свободный от этих недостатков, хотя требующий приведения исходной системы уравнений к специальному виду.
Для того, чтобы применить метод простой итерации, необходимо систему уравнений
Ax = b (3.22 )
с квадратной невырожденной матрицей A привести к виду
x = Bx + c, (3.23)
где B – квадратная невырожденная матрица с элементами bij, i, j = 1, 2, …, n, x – вектор-столбец неизвестных xi, c – вектор-столбец с элементами ci, i = 1, 2, …, n.
Существуют различные способы приведения системы (3.22) к виду (3.23). Рассмотрим самый простой. Представим систему (3.22) в развернутом виде:
 a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 n xn = b 1
a 11 x 1 + a 12 x 2 + a 13 x 3 + … + a 1 n xn = b 1
a 21 x 1 + a 22 x 2 + a 23 x 3 + … + a 2 n xn = b 2
a 31 x 1 + a 32 x 2 + a 33 x 3 + … + a 3 n xn = b 3 (3.24)
an 1 x 1 + an 2 x 2 + an 3 x 3 + … + annxn = bn
Из первого уравнения системы (3.24) выразим неизвестную x 1:
x 1 = a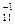 (b 1 – a 12 x 2 – a 13 x 3 – … – a 1 n xn),
(b 1 – a 12 x 2 – a 13 x 3 – … – a 1 n xn),
из второго уравнения – неизвестную x 2:
x 2 = a (b 2 – a 21 x 1 – a 23 x 3 – … – a 2 n xn),
(b 2 – a 21 x 1 – a 23 x 3 – … – a 2 n xn),
и т. д. В результате получим систему:
 x 1 = b 12 x 2 + b 13 x 3 + … + b 1 ,n- 1 xn- 1 + b 1 n xn + c 1
x 1 = b 12 x 2 + b 13 x 3 + … + b 1 ,n- 1 xn- 1 + b 1 n xn + c 1
x 2 = b 21 x 1 + b 23 x 3 + … + b 2 ,n- 1 xn- 1 + b 2 n xn + c 2
x 3 = b 31 x 1 + b 32 x 2 + … + b 3 ,n- 1 xn- 1 + b 3 n xn + c 3 (3.25)
.
xn= bn 1 x 1 + bn 2 x 2 + bn 3 x 3 + bn,n- 1 xn- 1 + cn
Матричная запись системы (3.25) имеет вид (3.23). На главной диагонали матрицы B находятся нулевые элементы, а остальные элементы вычисляются по формулам:
bij = 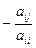 , ci =
, ci = 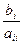 , i, j = 1,2, … n, i
, i, j = 1,2, … n, i 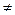 j. (3.26)
j. (3.26)
Очевидно, что диагональные элементы матрицы A должны быть отличны от нуля.
Выберем произвольно начальное приближение Обычно в качестве первого приближения берут x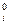 = ci или x
= ci или x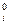 = 0. Подставим начальное приближение в правую часть (3.25). Вычисляя левые части, получим значения x
= 0. Подставим начальное приближение в правую часть (3.25). Вычисляя левые части, получим значения x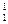 , x
, x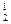 , …, x
, …, x . Продолжая этот процесс дальше, получим последовательность приближений, причем (k + 1)-е приближение строится следующим образом:
. Продолжая этот процесс дальше, получим последовательность приближений, причем (k + 1)-е приближение строится следующим образом:
|
|
|
x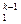 = b 12 x
= b 12 x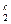 + b 13 x
+ b 13 x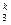 + … + b 1 ,n- 1 x
+ … + b 1 ,n- 1 x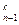 + b 1 n x
+ b 1 n x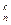 + c 1
+ c 1
 x
x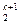 = b 21 x
= b 21 x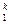 1 + b 23 x
1 + b 23 x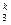 + … + b 2 ,n- 1 x
+ … + b 2 ,n- 1 x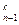 + b 2 n x
+ b 2 n x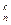 + c 2
+ c 2
x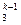 = b 31 x
= b 31 x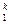 + b 32 x
+ b 32 x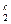 + … + b 3 ,n- 1 x
+ … + b 3 ,n- 1 x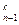 + b 3 n x
+ b 3 n x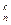 + c 3 … (3.27)
+ c 3 … (3.27)
x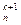 = bn 1 x
= bn 1 x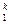 + bn 2 x
+ bn 2 x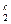 + bn 3 x
+ bn 3 x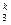 + bn,n- 1 x
+ bn,n- 1 x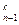 + c.n
+ c.n
Система (3.27) представляет собой расчетные формулы метода простой итерации Якоби.
Сходимость метода простой итерации. Известно следующее достаточное условие сходимости метода простой итерации Якоби.
Если элементы матрицы A удовлетворяют условию:
| aii | > 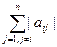 , i = 1, 2, …, n. (3.28)
, i = 1, 2, …, n. (3.28)
то итерационная последовательность xk сходится к точному решению x*.
Условие (3.28) называют условием преобладания диагональных элементов матрицы A, так как оно означает, что модуль диагонального элемента i- ой строки больше суммы модулей остальных элементов этой строки, i = 1, 2, …, n.
Необходимо помнить, что условие сходимости (3.28) является лишь достаточным. Его выполнение гарантирует сходимость метода простых итераций, но его невыполнение, вообще говоря, не означает, что метод расходится.
Справедлива следующая апостериорная оценка погрешности:
max| x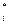 - x
- x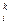 | £
| £ 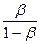 max| x
max| x – x
– x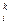 |, i = 1, 2, …, n, (3.29)
|, i = 1, 2, …, n, (3.29)
где b = max | bij | i, j = 1, 2, …, n.
Правую часть оценки (3.29) легко вычислить после нахождения очередного приближения.
Критерий окончания. Если требуется найти решение с точностью e, то в силу (3.29) итерационный процесс следует закончить как только на (k+ 1)-ом шаге выполнится неравенство:
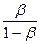 max| x
max| x – x
– x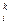 | < e, i = 1, 2, …, n. (3.30)
| < e, i = 1, 2, …, n. (3.30)
Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство
max| x – x
– x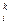 | < e 1, i = 1, 2, …, n. (3.31)
| < e 1, i = 1, 2, …, n. (3.31)
где e 1 = 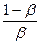 e.
e.
Если выполняется условие b £ 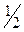 , то можно пользоваться более простым критерием окончания:
, то можно пользоваться более простым критерием окончания:
max| x – x
– x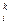 | < e, i = 1, 2, …, n. (3.32)
| < e, i = 1, 2, …, n. (3.32)
В других случаях использование критерия (3.32) неправомерно и может привести к преждевременному окончанию итерационного процесса.
|
|
|
Пример 3 .5.
Применим метод простой итерации Якоби для решения системы уравнений
 20.9x1 + 1.2 x 2 + 2.1 x 3 + 0.9 x 4 = 21.70
20.9x1 + 1.2 x 2 + 2.1 x 3 + 0.9 x 4 = 21.70
1.2x1 + 21.2 x 2 + 1.5 x 3 + 2.5 x 4 = 27.46
2.1x1 + 1.5 x 2 + 19.8 x 3 + 1.3 x 4 = 28.76 (3.33)
0.9x1 + 2.5 x 2 + 1.3 x 3 + 32.1 x 4 = 49.72
Заметим, что метод простой итерации сходится, т. к. выполняется условие преобладания диагональных элементов (3.28):
|20.9| > |1.2 + 2.1 + 0.9|,
|21.2| > |1.2| + |1.5| + |2.5|,
|19.8| > |2.1| + |1.5| + |1.3|,
|32.1| > |0.9| + |2.5| + |1.3|.
Пусть требуемая точность e = 10-3. Вычисления будем проводить с четырьмя знаками после десятичной точки.
 Приведем систему к виду (3.25):
Приведем систему к виду (3.25):
x 1 = – 0.0574 x 2 – 0.1005 x 3 – 0.0431 x 4 + 1.0383
x 2 = – 0.0566 x 1 – 0.0708 x 3 – 0.1179 x 4 + 1.2953
x 3 = – 0.1061 x 1 – 0.0758 x 2 – 0.0657 x 4 + 1.4525 (3.34)
x 4 = – 0.0280 x 1 – 0.0779 x 2 – 0.0405 x 3 + 1.5489
Величина b = max | bij |, i, j = 1, 2, 3,4 равна 0.1179, т. е. выполняется условие b £ 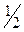 , и можно пользоваться критерием окончания итерационного процесса (3.32).
, и можно пользоваться критерием окончания итерационного процесса (3.32).
В качестве начального приближения возьмем элементы столбца свободных членов:
x = 1.0383, x
= 1.0383, x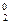 = 1.2953, x
= 1.2953, x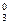 = 1.4525, x
= 1.4525, x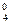 = 1.5489. (3.35)
= 1.5489. (3.35)
Вычисления будем вести до тех пор, пока все величины | x – x
– x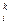 |, i = 1, 2, 3, 4, а следовательно, и max| x
|, i = 1, 2, 3, 4, а следовательно, и max| x – x
– x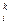 | не станут меньше e = 10-3.
| не станут меньше e = 10-3.
Последовательно вычисляем:
при k = 1
x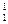 = – 0.0574 x
= – 0.0574 x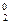 – 0.1005 x
– 0.1005 x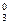 – 0.0431 x
– 0.0431 x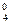 + 1.0383 = 0.7512
+ 1.0383 = 0.7512
x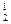 = – 0.0566 x
= – 0.0566 x – 0.0708 x
– 0.0708 x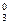 – 0.1179 x
– 0.1179 x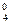 + 1.2953 = 0.9511
+ 1.2953 = 0.9511
x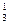 = – 0.1061 x
= – 0.1061 x – 0.0758 x
– 0.0758 x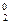 – 0.0657 x
– 0.0657 x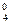 + 1.4525 = 1.1423
+ 1.4525 = 1.1423
x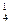 = –0.0280x
= –0.0280x – 0.0779x
– 0.0779x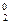 – 0.0405x
– 0.0405x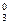 + 1.5489 = 1.3601
+ 1.5489 = 1.3601
при k = 2
x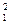 = 0.8106, x
= 0.8106, x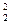 = 1.0118, x
= 1.0118, x = 1.2117, x
= 1.2117, x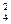 = 1.4077.
= 1.4077.
при k = 3
x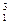 = 0.7978, x
= 0.7978, x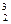 = 0.9977, x
= 0.9977, x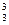 = 1.1975, x
= 1.1975, x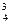 = 1.3983.
= 1.3983.
при k = 4
x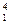 = 0.8004, x
= 0.8004, x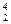 = 1.0005, x
= 1.0005, x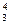 = 1.2005, x
= 1.2005, x = 1.4003.
= 1.4003.
Вычисляем модули разностей значений x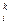 при k = 3 и k = 4:
при k = 3 и k = 4:
| x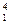 – x
– x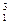 | = 0.026, | x
| = 0.026, | x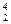 – x
– x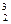 | = 0.028, | x
| = 0.028, | x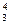 – x
– x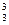 | = 0.0030, | x
| = 0.0030, | x – x
– x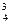 | = 0.0020.
| = 0.0020.
Так как все они больше заданной точности e = 10-3, продолжаем итерации.
При k = 5
x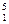 = 0.7999, x
= 0.7999, x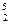 = 0.9999, x
= 0.9999, x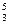 = 1.1999, x
= 1.1999, x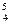 = 1.3999.
= 1.3999.
Вычисляем модули разностей значений x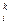 при k = 4 и k = 5:
при k = 4 и k = 5:
| x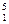 – x
– x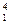 | = 0.0005, | x
| = 0.0005, | x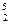 – x
– x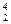 | = 0.0006, | x
| = 0.0006, | x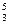 – x
– x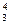 | = 0.0006, | x
| = 0.0006, | x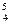 – x
– x | = 0.0004.
| = 0.0004.
Все они меньше заданной точности e = 10-3, поэтому итерации заканчиваем. Приближенным решением системы являются следующие значения:
x 1 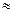 0.7999, x 2
0.7999, x 2 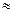 0.9999, x 3
0.9999, x 3 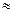 1.1999, x 4
1.1999, x 4 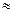 1.3999.
1.3999.
Для сравнения приведем точные значения переменных:
x 1 = 0.8, x 2 = 1.0, x 3 = 1.2, x 4 = 1.4.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 875; Нарушение авторских прав?; Мы поможем в написании вашей работы!